Проект «Математики в годы Великой Отечественной войны»

Содержание индивидуального исследовательского проекта по математике на тему «Математики в годы Великой Отечественной войны» отражает сведения в 11 классе о роли математики в те годы, а также о математиках, которые внесли огромный вклад в победу в ВОВ.

Проводя исследовательскую работу (проект) о математиках в годы Великой Отечественной войны учащийся 11 класса пришел к выводу о том, что советские математики вложили всю свою душу в работу для достижения великой победы. Их трудолюбие и самоотверженность удивляет и восхищает и сейчас.

Оглавление

Введение

1. Паспорт проекта.
2. Советские учёные и их открытия.
3. Оружие победы.

3.1. Т-34.
3.2. Авиация.

4. Математика на фронте.

Заключение
Используемая литература
Отзыв

«Смерть одного человека - это смерть, смерть двух миллионов только статистика».
Эрих Мария Ремарк.

«Великая Отечественная война была всенародной. И победа над врагом тоже была победой всенародной»
Константин Константинович Рокоссовский.

«Русские армии ценой незабываемой стойкости и неслыханных жертв уничтожили самую чудовищную военную машину, какую только видел мир».
Альбер Муссэ.

Вот уже 80 лет прошло с победы в Великой Отечественной войне. Победа над нацизмом нашего, советского народа, навсегда закрепилась в наших мыслях и сердцах. Эта победа стала одной из самых значимых в истории, и, если бы не она, то, возможно, мы, сейчас, жили бы иначе, чем сейчас.

В те тяжелые годы весь наш народ собрался, чтобы противостоять общей беде, в то время народ полностью отрицал все свои невзгоды, забыл о своих интересах и выгодах, все силы и мысли были направлены лишь ради одной цели - защитить Родину от неприятеля. В победу над врагом принимало множество людей, многие из них никогда даже не держали оружие в руках, но им это мешало воевать с хорошо подготовленным врагом.

На полях сражений воевали такие профессии, как врачи, механики, водители и даже спортсмены, но одними из самых ценных были математики. Математиков крайне часто отправляли в бой, но них была и другая задача, они обеспечивали техническую и стратегическую поддержку Родины.

В годы Великой Отечественной войны начали появляться новые, оригинальные и смелые технические решения. Это был глобальный подъем творческой мысли инженеров, и ученых, а также рабочих и конструкторов военной техники.

В годы Великой Отечественной войны патриотический лозунг: "Все для фронта, все для победы!", определил главный смысл работы каждого нашего человека, каждого ученого, конструктора, инженера.

Название проекта: «Математика в годы Великой Отечественной войны».
Руководитель проекта: Халилова Севиль Вейсовна.
Автор проекта: Бойко Никита Артемович.

Учебная дисциплина: Математика.
Тип проекта: познавательная деятельность

Цель работы: Понять какая роль была у математики в годы Великой Отечественной войны.

Задачи проекта:

• воспитать патриотизм у школьников.
• рассмотреть математику как средство ведения войны

Вопрос проекта:

• какую роль играла математика в годы Великой Отечественной войны?
• что делали математики в годы великой Отечественной войны?
• какие математики внесли значимый вклад в победу в Великой Отечественной войне?

Результат проекта: Разработка классного часа «Математика» для школьников, с целью воспитать патриотизм и привлечь внимания к техническим наукам и показать их значимость в условиях войны

Реализация проекта: Проведение классного часа «Математика» для школьников.

Математика – это наука, а каждая наука постоянно совершенствуется. Война, начавшаяся в 1941 году, не помешала этому процессу, и даже, напротив, стимулировала модернизацию математики, как науки. В годы войны советскими учёными были многочисленные математические и физические открытия. И сейчас я хочу привести примеры людей, которые воевали за нашу общую Родину с помощью математики.

Профессор С.В. Бахвалов, известный советский математик-геометр, разработал теорию приборов управления артиллерийским огнем, что помогало проще наводить орудия на врагов.

Н.Е. Кочин, советский учёный в области математике и механики, осуществил разработку и решение комплекса задач по «теории круглого крыла», что давало возможность, точно рассчитать силы, действующие на крыло самолёта во время полёта.

Видная роль в деле обороны нашей Родины принадлежит выдающемуся математику академику А.Н. Крылову. Он ещё в 1896 году опубликовал «Новую теорию качки кораблей на волнах и производимых этим движением напряжений» и она была использована нашими Военно-Морскими силами. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или иных отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен.

Лаврентьев Михаил Алексеевич, математик и механик, академик и вице-президент АН СССР, Герой Социалистического Труда, на начало великой Отечественной войны изучал действие на преграду металлического стержня, движущегося с большой скоростью. Позже в 1944 году вплотную занялся теорией кумулятивного действия. В конце войны он занимался расчётами водородной бомбы.

Труды одного из ведущих ученых математиков Анатолия Петровича Александрова позволили разработать метод размагничивания боевых и гражданских кораблей (испытания проводились на линкоре «Марат»). Все корабли Советского Союза, подвергались в портах «антимагнитной» обработке. Благодаря этому множество тысяч и военных, и гражданских моряков были спасены.

Фронт требовал увеличения эффективности огня артиллерии, повышения меткости стрельбы. Ее успешно решил академик А.Н. Колмогоров. Он выполнил работу о наиболее выгодном рассеивании снарядов при стрельбе по площадям. В исследовании А.Н. Колмогоров использовал плоскость, на которой он изучал разброс снарядов от начальной точки. Было доказано, что уклонение снарядов подчиняется особому закону распределения вероятностей - двумерному нормальному закону. Эта работа оказала серьезную помощь в повышении эффективности огня советской артиллерии.

Большое значение получили теории двух явлений – штопора и шимми (особые вибрации самолета, приводившие к его разрушению). Теорию этих явлений создал президент Академии наук СССР М.В. Келдыш. В результате практика полетов получила надежное средство для борьбы с шимми и штопором, и за все время войны в нашей авиации практически не было гибели самолетов и летчиков по этим причинам.

В апреле 1942г. коллектив математиков под руководством академика С.Н. Бернштейна разработал и вычислил таблицы для определения местонахождения судна по радиопеленгам. Таблицы ускоряли штурманские расчеты примерно в 10 раз.

Все математические исследования в комплексе с достижениями учёных из других областей науки позволили А.С. Яковлеву и С.А. Лавочкину создать грозные истребители, С.В. Илюшину – неуязвимые штурмовики, А.Н. Туполеву, Н.Н. Поликарпову – мощные бомбардировщики, заметно увеличить их скорость. На основе работ учёных – математиков проводились важнейшие расчеты на прочность не только самолётов, но и танков, артиллерийских систем. Эти работы имели большое значение и для строительной механики.

В самом начале войны все самолеты, находившиеся на вооружении Советского Союза, безнадежно устарели и были не пригодны для боя с более совершенной немецкой авиацией, и эту проблему начали сразу же решать, разрабатывали новые модели и прототипы всевозможной авиации. Лидирующую роль в исследованиях занимали, конечно же, наши математики и инженеры.

Работа шла в ускоренном режиме, и скоро появились совершенно новые самолёты, которые если давали преимущество над противником. Владение воздушными территориями имело огромное тактическое значение для Советской армии. Также Советская армия и сама получила возможность проводить бомбардировки, что не давало фашистской армии использовать батальоны артиллерии.

Доминирование в воздухе означало полное видение боя и бесценные разведданные. В истребительной авиации ВВС перед началом войны велись исследования новой авиационной техники.

Результатом этого стало появление таких самолетов как Як-1, ЛаГГ-3 и Миг-3. Они заменили старые истребители И-16 и И-153. В ходе войны новые модели постоянно модифицировались, чтобы держать темп с фашистской Германией.

В бомбардировочной авиации на первых порах использовался ДБ-40, который благодаря аэродинамическим наработкам наших математиков и особой конструкции смог поставить целых 5 мировых рекордов, в первую очередь - из-за его рекордно долгих перелетов, хотя практика показала критическую слабость самолета. А именно - его очень большую уязвимость в воздухе из-за слабой брони и отсутствия серьезного вооружения, что, к сожалению, поставило крест на идее дальних бомбардировок.

Но советские инженеры не стали отчаиваться и приняли решение сделать упор на скорости и моментальности бомбардировок, делая новый самолет - Пе-2 пикирующим. Идея оказалось удачной, Пе-2 пришелся по вкусу начальству и начал массово производиться с самого начала войны.

К началу Войны у Советского Союза на вооружении было около 20 тысяч танков, но большинство из них были лёгкие танки (Т-26, Бт-2, Бт-5, Бт-7 и Т-70). Советское руководство понимало, что лёгкие танки не смогут долго биться со средними и тяжелыми танками Германии и поручили сначала Ленинградскому, а затем Харьковскому конструкторскому бюро разработать танк, который смог бы конкурировать с танками Германии. И этим танком стал - Т-34.

В этом танке сочеталось всё: был очень дешёвый для своего времени, благодаря чему он и стал самым массовым за всю Вторую Мировую войну, имел хорошее орудие, которое пробивало большинство танков Германии того времени и имел хорошую броню, которую немецкие танки не могли пробить.

И именно благодаря математикам были проведены точные расчёты, которые сделали этот танк легендарным.

Уникальные особенности конструкции Т-34:

Наклонная броня.
Продуманная схема бронирования корпуса и башни танка с широким применением наклонной брони, которая позволяет значительно повысить защиту танка от пробития снарядом не за счет увеличения толщины металла, а за счет его простого наклона под углы 30-60 градусов.

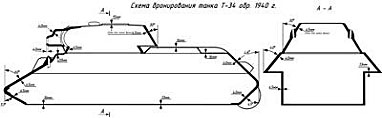
Конструкторы танка путем не сложных математических расчетов с применением формул тригонометрии подсчитали, что если лист брони толщиной 45 мм установить в лобовой броне танка не под прямым углом, а под углом 60 градусов, то снаряду выпущенному врагом по танку нужно будет преодолеть толщину стали уже на 45 мм, а 90мм. Гениально!!! Так была создана оптимальная, математически просчитанная форма корпуса танка. При этом танк не перегружается лишним весом от толстой брони и приобретает столь важную в современной войне скорость и маневренность. Что не скажешь об аналогичных немецких танках.

Ниже показана наклонная броня на Т-34.

Ниже приведена схема бронирование немецкого PZkpf -IV. Обратите внимание на угловатость форм танка в боковой проекции, то есть немецкие конструкторы полностью проигнорировали простой и эффективный способ защиты танка без увеличения толщины брони.  

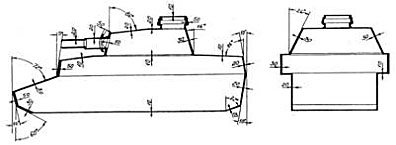
Широкие гусеницы.
В 1940-м году проводили расчёты площади простейших фигур. Зная массу танка и размеры гусениц можно определить с какой силой давит танк на поверхность земли – кг/см2. Удивительно, но большой и тяжелый танк за счет широких гусениц давит на грунт примерно также как и взрослый человек! Это значит, что он может проехать там, где пройдет человек, но не проедет автомобиль и не пройдет всадник на лошади.

На рисунке ниже показаны значения давления на грунт на различных примерах.

Сравнение ширины гусениц немецкого PZ kpfw -IV (слева)  и советского Т-34 (справа)

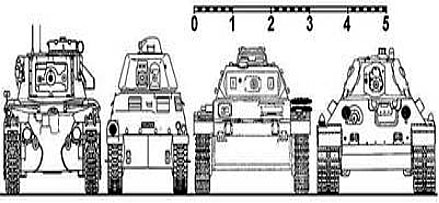
Из-за широких гусениц, Т-34 создавал большую площадь опоры на землю и громадная масса стального танка распределялась на большей площади чем у немецкого танка, поэтому Т-34 значительно меньше давил на грунт и мог проехать там где немецкий танк проваливался и застревал, особенно это сказывалось в период весеннего бездорожья и в болотах

Математический расчет удельного давления на грунт для Т-34:
Исходные данные: Ширина гусеницы (а) – 50 см., длина опорной на грунт  части гусеницы (b) – 414 см., масса танка (m) – 26 5000 кг.

Расчет :

1. Определяем площадь (S) гусениц которые в пятне контакта на грунт имеют форму прямоугольника, тогда S = a*b=50*414=20700 см2. Так как гусениц у танка две, общая площадь опоры танка на грунт составит 2*20700=41400м2.
2. Определяем удельное давление танка на грунт- F(кг/см2): F=26500/41400=0,64
3. Вывод: Значение 0,64 кг/см2 близко давлению на грунт создаваемое  взрослым человеком (0,6 кг/см2), к чему и стремились создатели Т-34, так как понимали, что танк должен проехать там где пройдет солдат пехотинец, это позволит пехоте и танкам наступать на противника вместе, что очень важно.
4. Математический расчет удельного давления на грунт для немецкого PZkpf -IV:
5. Исходные данные: Ширина гусеницы (а) – 38 см., длина опорной на грунт  части гусеницы (b) – 405 см., масса танка (m) – 25 000 кг.

Расчет:

6. Определяем площадь (S) гусениц которые в пятне контакта на грунт имеют форму прямоугольника, тогда S = a*b=38*405=15390 см2. Так как гусениц у танка две, общая площадь опоры танка на грунт составит 2*15390=30780м2.
7. Определяем удельное давление танка на грунт- F(кг/см2): F=25000/30780=0,81

Вывод: Значение 0,81 кг/см2 выше чем у Т-34, это означает, по проходимости по бездорожью немецкий танк уступал советскому танку.

Мощный двигатель
Мощный двигатель очень важен для танка, он позволяет танку внезапно атаковать противника, маневрировать, уклоняясь от огня противотанковых средств противника и также стремительно уходить из зоны обстрела.

Мощность двигателя измеряется в лошадиных силах. Скорость  и манёвренность танка напрямую зависит от того на сколько мощность двигателя соответствует его массе, этот показатель называется удельная мощность двигателя и измеряется в л.с на 1 тонну массы, то есть сколько лошадиных сил приходятся на том чтобы перемещать одну тонну массы танка.

Двигатель Т-34 имел мощность 500 лошадиных сил, а масса танка составляла 26,5 тонны. Путем простых математических расчетов получаем, что Т-34 на одну тонну массы приходилось 18,9 лошадиных сил (500/26,5=18,9), а для немецкий Pzkpf-4 – 10,9 лошадиных сил на 1 тонну  (272 разделить 25).

Это означает, что при Т-34 имел почти в 2 раза более высокий показатель удельной мощности чем у немецкого танка, за счет более мощного двигателя и  следовательно был гораздо более быстрый и подвижный на поле боя. Этого и добивались советские конструкторы, которые понимали, что в умелых руках наших танкистов, быстрый и манёвренный танк будет очень трудной мишенью для врага.

Многие ученые и математики были мобилизованы или ушли на фронт добровольцами. В тяжелые дни для страны они показали себя верными и обязанными Родине, готовыми на самопожертвование, и отдать всего себя во благо и освобождение своей Родины. Многие не смогли вернуться домой к своим жёнам и детям.

Давайте возьмём для примера советских снайперов: Ивана Михайловича Сидоренко, Михаила Ильича Суркова, Василия Григорьевича Зайцева и других. Все они обычно работали на дальних дистанциях и для того, чтобы обезвреживать врагов им приходилось очень часто обращаться к математике.

Они рассчитывали баллистический коэффициент - числовую величину, характеризующую способность пули сохранять скорость и направление полета вопреки сопротивлению воздуха. Это размерная величина, пропорциональная массе тела, делённой на произведение коэффициента сопротивления аэродинамических сил на характерную площадь. БК поможет нам определить самую лучшую позицию для стрельбы.

Вычислим его по формуле:

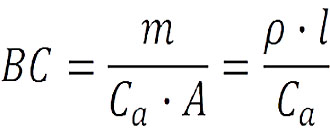
, где BC – баллистический коэффициент, M – масса, A – площадь поперечного сечения, C(d) – коэффициент сопротивления аэродинамических сил, p – средняя плотность и L – длина тела (пули).

Масса советской снайперской пули 7,62×54 мм R была примерно 9.6 грамма, площадь поперечного сечения 0.6 кв. см., коэффициент аэродинамических сил 0.5. Рассчитаем баллистический коэффициент. Он равен 32. К сравнению БК пистолетной пули равен 1.
Баллистический коэффициент мы используем для нахождения идеальной позиции для стрельбы. Оружие с низким БК рассчитано на применение в ближнем бою, а с высоким – для дальнего поражения целей. Основываясь на таблицах, мы находим оптимальное расстояние – 500 - 1000 метров.

Для вычисления поправки на дальность, у каждого снайпера есть таблица результатов пристрелки своего оружия/патрона на разные дистанции, как правило, через каждые 50 метров/ярдов. В ней, как минимум, записаны поправки на дальность и поправки на ветер. Надо так же понимать, что результаты «холодного ствола» и «горячего ствола» дают разные результаты и лучше иметь обе таблицы. Есть два способа вычислить поправку на ветер. Один из них учитывает знание данных из баллистических таблиц снайперов, а другой – геометрическую формулу.

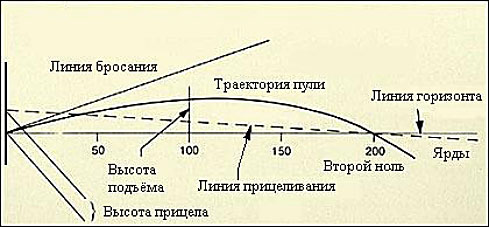
Создается треугольник с прямым углом между катетами, где расстояние до цели будет одним из катетов. Направление ветра становится гипотенузой, точнее углом между гипотенузой и катетом. Гипотенуза вычисляется по формуле Пифагора. Возьмем расстояние в ярдах, потому что они приняты за основу практически каждой формулы. Пусть расстояние будет равно 700 ярдам. Тогда гипотенуза будет равна примерно 990 ярдам. Теперь рассчитаем синус: 0.707 или √0.5 (постоянное значение для угла 45 градусов). Ну а теперь нужно умножить его на боковую поправку в 23 дюйма. 0,707 * 23 ≈ 16,26 дюйма. Учитывая все вычисления, переводим все в угловые минуты и оптимально наводим прицел.

В ходе исследовательского проекта по математике на тему «Математики в годы Великой Отечественной войны», я убедился, что математика важнейшая точная наука, которая является неотъемлемой частью нашей жизни, почти все, что нас окружает можно описать универсальным языком математики. Прорыв в технологиях в 20 веке также был бы не возможен без применения развития математики как средства сложнейших расчетов простых и сложных конструкций, физических явлений, технологических процессов, программного обеспечения.  

Не стала исключением и военная сфера в один из драматических периодов истории нашей страны – Великая Отечественная война. Я узнал, какую роль сыграли ученые математики в годы войны, от личного участия в боевых действиях, до кропотливой работы в конструкторских бюро  по проектированию и созданию новейших вооружений необходимых фронту.

Из всего вышесказанного можно сделать вывод, что советские математики вкладывали всю свою душу для достижения великой победы. Остаётся лишь удивляться и восхищаться их трудолюбию и самоотверженности.

1. В.Н. Шунков «Красная армия». Москва. Харвест. 2016.
2. В.Н. Шунков «Вермахт». Москва. Харвест. 2016.

на проектную работу обучающегося 11 «Б» класса
Федерального Государственного Казённого
Общеобразовательного Учреждения «СОШ №6»
Бойко Никиты Артёмовича.

По теме: Математика в годы Великой Отечественной Войны.

Работа, представленная на рецензирование, относится к учебной дисциплине «математика» и посвящена сложному вопросу рассмотрению математике в годы ВОВ. Тема автором выбрана не случайно. Никита воспитывается в семье военнослужащих и хочет пойти по стопам отца, связать судьбу с профессией военного. Также работа выполнялась к 80-летию Победы в Великой Отечественной войне.

В работе проанализирована история развития математики в военном деле, проведен сравнительный анализ техники, используемой на полях битвы, высказано свое отношение к событиям того времени и к участникам этих событий.

Структура проекта соблюдена. Автором проекта верно определены цели и задачи проведённой работы, сформулирована её актуальность. Ценность работы в том, что ученик объединил данные многих исследований, представил расчеты и чертежи, иллюстрации. И все это в удобном для школьников формате. Присутствует и исследовательская часть работы. Работа структурирована, логична, последовательно изложена.

Автор проекта демонстрирует осведомлённость в самых разных дисциплинах и способность практически объединять их, владеет математической теорией. Он представил основные математико-философские вопросы и мысли именитых деятелей, современных исследователей.

Литературные источники, используемые для выделения проекта, указаны, правила их оформления соблюдены.
Вывод: проектная работа Бойко Н.А. по теме «Математика в годы Великой Отечественной Войны» отвечает требованиям, предъявленным к индивидуальному проекту, рекомендуется к защите.