В индивидуальном исследовательском проекте по математике на тему "Различные способы решения систем линейных уравнений" обучающаяся 11 класса описала основные моменты из истории жизни ученых, которые в различные периоды занимались этим вопросом, а также классифицировала и описала каждый из существующих методов решения, приводя наглядные примеры решения задач с их помощью.

Подробнее о работе:

В исследовательской работе по математике на тему «Различные способы решения систем линейных уравнений» учащаяся 11 класса сделала выводы о том, что графический метод решения удобнее для системы из двух линейных уравнений, а метод Гаусса менее пригоден для этого, с точки зрения наглядности.

Проводя исследовательскую работу в рамках индивидуального проекта о различных способах решения систем линейных уравнений, ученица 11 класса провела анкетирование среди учащихся 9-х классов по вопросам изучения методов решения систем линейных уравнений, систематизировала полученные данные и представила их в виде диаграмм. Благодаря полученным знаниям, учащаяся 11 класса знает как сэкономить время и правильно решить задачу на основе оптимального метода решения.

Оглавление

Введение
Глава I. Исследовательская историческая часть
1.1. История вопроса. Сферы применения
1.2. Ученые, которые работали в этой сфере
1.3. Диофант Александрийский
1.4. Гаусс Карл Фридрих
1.5. Габриэль Крамер
1.6. Мухаммед ибн Муса аль-Хорезми
Глава II. Исследование методов и примеры решения
2.1. Методы решения систем линейных уравнений
2.2. Метод подстановки
2.3. Метод уравнивания коэффициентов (способ сложения)
2.4. Метод сравнения
2.5. Графический метод
2.6. Метод Гаусса
2.7. Метод Крамера (метод определителей)
Заключение
Литература

Проектная деятельность – совместная творческая деятельность учащихся и преподавателей, имеющая общую цель, направленная на углубленное изучение темы в данной предметной области, совершенствование навыков владения техническими средствами ИКТ и практического решения задач.

Математика признана интеллектообразующим учебным предметом. Знания, умения и навыки, полученные на уроках математики, развиваются, расширяются, углубляются, находят практическое применение на других предметах и в жизни. Много сейчас говорят о прикладной математике.

И учитель, и ученик переживают вдохновение творчества, расширяют границы знаний, развивают творческую деятельность, учатся самостоятельно принимать решения по возникающим вопросам. В итоге ученики пробуют свои силы, проявляют свою индивидуальность, показывают публично свой достигнутый результат. Это имеет важное прикладное значение, носит практический характер.
Чтобы преуспеть в любой деятельности, человек должен обладать достаточным интеллектом, который включает в себя умение логически мыслить, способность обобщать и делать выводы, быстро и правильно принимать решения.

Тема “Исследование систем линейных уравнений разными методами” выбрана не случайно. Выбор обусловлен тем, что избранный материал непосредственно связан с вопросами, которые изучаются на протяжении всего курса алгебры основной и старшей школы. Данный материал доступен и дает возможность хорошо подготовиться к выпускным и конкурсным экзаменам. Данная тема встречается в КИМах ОГЭ как самостоятельное задание и в текстовых задачах на составление систем уравнений. Текстовые задачи на составление систем уравнений есть в КИМах ЕГЭ (задача №11) в 11 классе. Изучение выбранной темы позволит успешно начать обучение в вузе по линейной алгебре.

Системы уравнений с двумя переменными мы начали решать в 7 классе. Выполняя контрольную работу КИМов ОГЭ за 9 класс демонстрационного варианта №6, я встретилась с ситуацией, когда задача решается с помощью составления системы трех уравнений с тремя неизвестными.
В-6 №22 (аналогичные задачи В-35 №22; В-36 №22). Задача: Игорь и Паша красят забор за 10 часов, Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь вместе красят за 15 часов. За сколько часов мальчики покрасят забор, работая втроём?
И + П = 1 И + П + В = 1
П + В = 1
В + И = 1

Аннотация работы: В работе рассмотрены различные математические методы решения систем линейных уравнений, показаны алгоритмы и примеры решения линейных алгебраических уравнений различными методами. Дается краткая историческая справка о жизни ученых, занимавшихся данной проблемой. Приводятся примеры использования СЛАУ. Данная тема способствует формированию математической интуиции, которая поможет ориентироваться в способах решения систем.

Целью работы является оценка различных методов решения систем линейных уравнений с точки зрения вычислительной сложности.

Задачи:

• Обобщение методов решения СЛАУ, знакомых с 7 класса;
• Знакомство с новыми методами решения СЛАУ;
• Изучение истории вопроса (развития теории, имена ученых, их достижения).

Актуальность и новизна: подготовка к экзаменам: как сэкономить время и правильно решить задачу на основе оптимального метода решения.
Ключевые слова и понятия: системы линейных уравнений, решение системы, методы решения, исследование решений.

Было проведено анкетирование среди учащихся 9-х классов по вопросам изучения методов решения систем линейных уравнений.
Результаты анкетирования таковы:

Какие методы решения СУ ты знаешь?

Какими методами при решении систем уравнений чаще пользуешься?

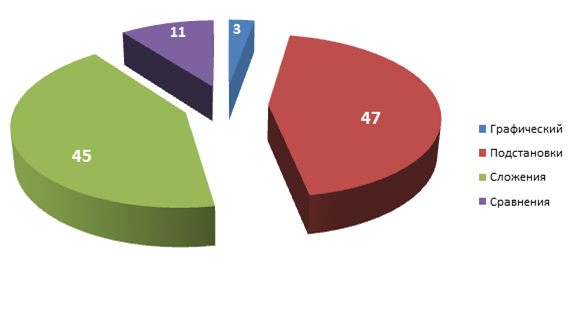
Какие методы решение СУ на твой взгляд самые легкие и быстрые?

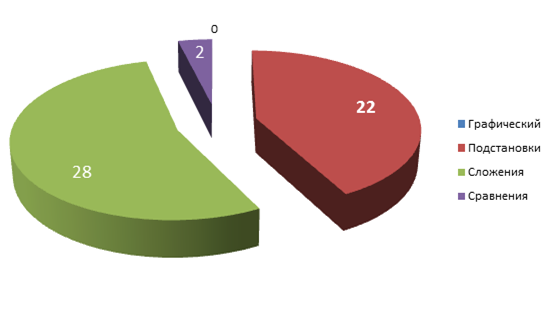
Результаты анкетирования показали, что ребята знают методы решения систем уравнений, изучаемые в школе. Преимущество отдают методам подстановки и алгебраического сложения. Других методов они не знают.
И для меня стало интересно изучить методы решения систем, в которых больше двух уравнений и больше двух неизвестных.

Во все времена математика была основой научно-технического и экономического развития народов. Она была и есть тем микроскопом, который позволяет проникать в дебри знаний, составляющих основу нашей цивилизации. Эта роль математики особенно важна в наше время.
Суть математики состоит в том, чтобы подробно изучить и рассмотреть науку о числах и все те действия, которые над числами производятся.

Возникновение числа и счета - длительный процесс в истории человечества. Развивалось общество - совершенствовались и научные представления, постепенно складываясь в стройную систему математических знаний. Основой этих знаний стало решение уравнений.

Самые ранние сведения о возникновении алгебры в виде правил решения уравнений мы встречаем у вавилонян в III–II вв. до н. э. В вавилонской математике появляется числовая алгебра в виде решения уравнений и систем уравнений первой и второй степени. Египтяне сильно отстали от вавилонян в решении уравнений. Они не решали уравнения, но решали задачи, которые требовали применения уравнений первой степени. Они решались приемом, который позднее через арабов перешел к европейским народам. Это - способ решения задач методом предположений, или “фальшивое правило”, как его назвал Леонтий Филиппович Магницкий в “Арифметике”.

Решение уравнений первой степени требует знаний о числах: натуральных, дробных, отрицательных. Для решения уравнений степени выше первой знаний должно быть больше. Так шло и развитие алгебры. Усложняющиеся уравнения требовали для своего решения новых чисел.
Уравнения, содержащие более одного неизвестного, или система уравнений, в которой число неизвестных больше числа уравнений, называются неопределенными уравнениями. Решением таких уравнений в целых числах занимался Диофант.

Слово “алгебра”, как название части математики, появилось у математиков Средней Азии и арабских стран в IX веке нашего летоисчисления. Термин “алгебра” пришел к нам из Средней Азии, города Хорезма.

Диофант Александрийский (др.-греч. Διόφαντος ὁ Ἀλεξανδρεύς; лат. Diophantus) - древнегреческий математик, живший предположительно в III веке н. э. Нередко упоминается как «отец алгебры». Автор «Арифметики» — книги, посвящённой решению алгебраических уравнений.

Диофант был первым греческим математиком, который рассматривал дроби наравне с другими числами. В наше время под «диофантовыми уравнениями» обычно понимают уравнения с целыми коэффициентами, решения которых требуется найти среди целых чисел. Диофант также одним из первых развивал математические обозначения.

О подробностях его жизни практически ничего не известно. С одной стороны, Диофант цитирует Гипсикла (II век до н. э.); с другой стороны, о Диофанте пишет Теон Александрийский (около 350 года н. э.), — откуда можно сделать вывод, что его жизнь протекала в границах этого периода. Возможное уточнение времени жизни Диофанта основано на том, что его Арифметика посвящена «достопочтеннейшему Дионисию». Полагают, что этот Дионисий — не кто иной, как епископ Дионисий Александрийский, живший в середине III в. н. э.
Основное произведение Диофанта — Арифметика в 13 книгах. К сожалению, сохранились только 6 первых книг из 13.

Гаусс Карл Фридрих - знаменитый немецкий математик.
Родился 23 апреля 1777 года в Брауншвейге и с раннего возраста обнаружил выдающиеся математические способности.

Рассказывают, что, будучи трех лет, Гаусс решал числовые задачи и любил чертить геометрические фигуры. Юный вычислитель был представлен герцогу Карлу Вильгельму Фердинанду Брауншвейгскому и нашел в нем покровителя, принявшего живое участие в его воспитании.

Еще не достигнув 25-ти лет, Гаусс выступил с знаменитым трактатом по теории чисел: "Disquisitiones arithmeticae" (1801). По богатству материала, ряду прекрасных открытий, разнообразию и остроумию доказательств это сочинение до сих пор считается основным при изучении теории чисел. Между прочим, укажем на прекрасную теорию двучленных уравнений в этом сочинении, показывающую, что можно при помощи циркуля и линейки вписать в круг правильный семнадцатиугольник.

Продолжая занятия на теорию чисел, а также и другими отраслями анализа, Гаусс публикует ряд солидных работ по астрономии. Гаусс всегда стремился к оригинальности; затрагивая уже ранее разрабатывавшийся вопрос, казалось, что ученый не знаком с предшествовавшими работами, так оригинальны приемы и формы, которые Гаусс придавал изложению. К сожалению, эта оригинальность методы при излишней лаконичности изложения делает многие места сочинений Гаусса весьма трудными для читателя.

Замечательная способность Гаусса к числовым выкладкам обнаружилась во многих его работах, о чем свидетельствуют посмертные рукописи, как, например, таблица превращения в десятичные обыкновенных дробей со знаменателем меньшим 997. Большого труда стоили автору также таблицы для счета классов квадратичных форм и разложения на множителей чисел вида: а2+1, а2+4, а2+9,... а2+81. Карл Фридрих Гаусс умер 23 февраля 1855 года.

Швейцарский математик, ученик и друг Иоганна Бернулли, один из создателей линейной алгебры Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария), в семье врача. Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.

В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Юноша так понравился магистрату, что специально для него и ещё одного кандидата на место преподавателя была учреждена отдельная кафедра математики, где Крамер и работал в последующие годы. Талантливый учёный написал множество статей на самые разные темы: геометрия, история, математика, философия. В 1730 году он опубликовал труд по небесной механике.

Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера. Габриэль Крамер скончался 4 января 1752 года во Франции.

Мухаммад ибн Муса аль-Хорезми (783-850) родился и вырос в древнем Хорезме. Начальное образование он получил в родном городе. Его наставниками были выдающиеся ученые Мавераннахра и Хорезма.

С именем аль-Хорезми связана большая научная работа в академии ал-Маъмуна. Известно, что он попал в Багдад уже вполне сложившимся ученым, последователем индийской научной школы, которая проникла в Среднюю Азию вместе с буддизмом. Аль-Хорезми был хорошо знаком и с греческой наукой. Он возглавил багдадский "Байт ал-хикма", а его сотрудниками были ученые из Сирии, Египта, Персии, Хорасана и Мавераннахра. Совместно с ними он по приказу халифа в пустыне Санджар проводил специальные измерения длины градуса дуги земного меридиана с целью определения размеров земного шара. Эти измерения на протяжении 700 лет оставались не превзойденными по точности. При активном участии аль-Хорезми была составлена знаменитая карта ал-Маъмуна.

Эта географическая карта, дошедшая до наших дней, содержала ценные сведения о материках и морях, обитаемых землях и пустынях, горах, реках и их истоках, о городах и селениях. В ней были также астрономические сведения. Математический труд аль-Хорезми еще в XII веке был переведен с арабского на латинский язык. Затем были сделаны переводы на новые европейские языки, и на их основе создавались различные учебники по математике.

Благодаря переводам на латынь книги аль-Хорезми индийская десятичная позиционная система счисления стала известна в Европе и сыграла важную роль в становлении науки эпохи Возрождения. Таким образом, аль-Хорезми, заложив основы алгебры, превратил ее в самостоятельную науку и оказал плодотворное влияние на развитие средневековой научной мысли в странах Востока и Запада.

Метод решения хорош, если с самого начала
мы можем предвидеть - и далее подтвердить это, -
что, следуя этому методу, мы достигнем цели.
Г. Лейбниц

Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных.
Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно.

Решение системы уравнений — это последовательность чисел (k1, k2, ...,kn), которая является решением каждого уравнения системы, т.е. при подстановке в каждое уравнение этой системы вместо переменных x1, x2, ..., xn, дает верное числовое равенство. Решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто.

Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.
К решению систем уравнений сводятся многие задачи, связанные с реальной жизнью, например, на работу, на движение.

С методами решения систем линейных уравнений мы встретились в 7 классе. И для системы уравнений, состоящей из двух уравнений с двумя неизвестными, мы познакомились с такими методами решения систем:

• Графический метод;
• Метод подстановки;
• Метод коэффициентов (или алгебраического сложения).

Тогда, в 7 классе, нас познакомили с таким методом, как правило Крамера. Для этого мы познакомились с понятием определитель и правилами его вычисления. Интересный и быстрый метод. Научившись вычислять определители третьего порядка, можно решить систему из трех уравнений с тремя неизвестными.

Одним из эффективных методов решения систем линейных уравнений - это метод Гаусса, метод последовательного исключения неизвестных для перехода к равносильной системе, в матрице коэффициентов.

Таким образом, есть еще два способа

• Метод Крамера
• Метод Гаусса и матричная форма.

Вспомним известные из школьного курса математики методы решения систем уравнений с несколькими переменными, чтобы потом ответить на вопрос, какие методы будут самыми удобными, простыми и быстрыми в использовании

Рассмотрим один из алгебраических способов решения системы линейных уравнений, методом подстановки. Он заключается в том, что используя первое выражение, мы выражаем y, а затем подставляем полученное выражение во второе уравнение, вместо y. Решая уравнение с одной переменной, находим x, а затем, при обратной подстановке, и y. Этот метод, как универсальный, используется при решении любых систем уравнений с двумя неизвестными второй, третей степени.

Например:

Таким образом
Способ подстановки (алгоритм):

• Из какого-либо уравнения выразить одну переменную через другую.
• Подставить полученное выражение для переменной в другое уравнение и решить его.
• Сделать подстановку найденного значения переменной (обратная подстановка) и вычислить значение второй переменной.
• Записать ответ: х =…; у=… . или (хо; уо)

Метод уравнивания коэффициентов (способ сложения) основан на свойстве суммы противоположных чисел, когда за счет алгебраического сложения исчезает одна переменная, и остается уравнение с одной переменной.

Например:

Способ сложения (алгоритм)

• Уравнять модули коэффициентов при какой-нибудь переменной.
• Сложить почленно уравнения системы.
• Составить новую систему: одно уравнение новое, другое - одно из старых.
• Решить новое уравнение и найти значение одной переменной.
• Подставить значение найденной переменной в старое уравнение и найти значение другой переменной.
• Записать ответ: х =…; у =… .

Метод сравнения основан на свойстве равенства частей уравнений, когда за счет приравнивания их исчезает одна переменная, и остается уравнение с одной переменной. Чаще всего этот способ применяют при решении математической задачи: найти координаты точек пересечения графиков функций: у = 3х – 7 и у = -2х + 6.
Отсюда, т.к. у = у, значит, 3х -7= -2х + 6.

Способ сравнения (алгоритм)

• Выразить у через х (или х через у) в каждом уравнении.
• Приравнять выражения, полученные для одноимённых переменных.
• Решить полученное уравнение и найти значение одной переменной.
• Подставить значение найденной переменной в одно из выражений для другой переменной и найти её значение.
• Записать ответ: х =…; у =… .

Впервые определение функции было дано гениальным русским математиком Н.И. Лобачевским, термин “функция” введен Лейбницем. Символическая запись в виде формулы впервые введена Л. Эйлером. Из определения функции следует, что необходимо указать два множества чисел (значений аргумента и функции) и закон соответствия между ними, это может быть сделано графически. Такой способ применяют в естествознании, технике (при использовании самопишущих приборов).

Графическое представление функций позволяет приближённо решить любое уравнение с одним неизвестным и систему двух уравнений с двумя неизвестными. Чтобы решить систему двух уравнений с двумя неизвестными x и y, мы рассматриваем каждое из уравнений как функциональную зависимость между переменными x и y и строим графики этих двух функций. Координаты точек пересечения этих графиков дают нам искомые значения неизвестных x и y (т.е. решение этой системы уравнений).

Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.

Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.

Так как этот метод дает все-таки приближенные значения, то он очень удобен при решении математической задачи или исследования с такой постановкой вопроса: Сколько решений имеет система? Решение определяется количеством точек пересечения графиков уравнений, входящих в систему уравнений.

Например:
Решим графическим способом систему уравнений, используя алгоритм:
2х – у = 3;
х – у = -1;

Решением системы являются координаты
точек пересечения графиков уравнений
2х – у = 3 и х – у = -1, представляя их
в виде функций у = 2х – 3 и у = х + 1.
Имеется одна точка пересечения,
значит, система имеет одно решение.

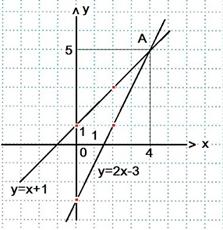
Ответ: (4; 5)

Метод Гаусса - это универсальный метод исследования и решения произвольных систем линейных уравнений. Он состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных с помощью элементарных преобразований, не нарушающих эквивалентности систем. Переменная считается исключенной, если она содержится только в одном уравнении системы с коэффициентом 1.

Метод Гаусса решения системы n линейных уравнений с n переменными представляет систематизированную схему последовательного исключения переменных.

Например:
Этот метод широко применяется в практике вычислений при решении уравнений с большим количеством неизвестных.

Для решения систем уравнений применяют метод Гаусса, названный так в его честь. Этот метод применяется в практике вычислений при решении систем линейных уравнений с большим количеством неизвестных, Гаусс дал строгое доказательство существования корней у всякого уравнения, однако это не означало, что для нахождения корня можно вывести формулу.
Метод Гаусса основан на использовании матрицы, составленной из коэффициентов неизвестных, преобразованной к единичной «треугольного» вида с помощью преобразований.

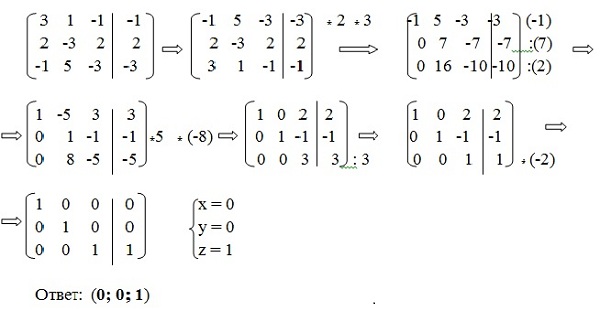
Этот метод широко применяется в практике вычислений при решении уравнений с большим количеством неизвестных.

Достоинства метода Гаусса и недостатки:

• менее трудоёмкий по сравнению с другими методами;
• применим к любой системе линейных уравнений;
• позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение;
• позволяет найти максимальное число линейно независимых уравнений - ранг матрицы системы;
• в силу простоты и однотипности выполняемых операций пригоден для счета на электронно-вычислительных машинах.

Рассмотрим задачу из ОГЭ (КИМы, вариант 6, №22) и ЕГЭ (КИМы, задача №11): Игорь и Паша красят забор за 10 часов, Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь вместе красят за 15 часов. За сколько минут мальчики покрасят забор, работая втроём?

Ме́тод Кра́мера (правило Крамера) — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно).

Метод Крамера - метод определителей (алгоритм):

• Составить табличку (матрицу) коэффициентов при неизвестных и вычислить основной определитель .
• Найти - определитель x, получаемый из  заменой первого столбца на столбец свободных членов.
• Найти - определитель y, получаемый из  заменой второго столбца на столбец свободных членов.
• Найти значение переменной х по формуле x / .
• Найти значение переменной у по формуле y / .
• Записать ответ: х =…; у =… .

Метод Крамера удобен в получении ответов, когда значения переменных получаются НЕ целыми числами, и их очень трудно использовать в методах подстановки.
Решим задачу про мальчиков, которые красили забор, из указанных КИМов ОГЭ и ЕГЭ.

Определим, за сколько часов мальчики вместе выполнят всю работу, приняв всю работу за 1:
1 : 1/8 = 8 (часов) требуется мальчикам для покраски забора, работая втроём, если она будут работать вместе.

В типовых заданиях по математике в сборнике «Я сдам ОГЭ» по алгебре для 9 класса встречаются такие задания.

При работе над данным исследовательским проектом на тему "Различные способы решения систем линейных уравнений" прослежено развитие алгебры на протяжении 2,5 тысяч лет, накоплен банк задач, решенных разными методами. Исследованы методы решения систем уравнений. Например, графический метод решения более удобен для системы из двух линейных уравнений (наглядно и быстро), а метод Гаусса для этой цели менее пригоден. Он проигрывает с точки зрения наглядности. Однако, именно метод Гаусса и метод Крамера являются наиболее универсальными для решения систем уравнений с большим количеством уравнений и переменных.

Исследовательская работа по математике на выбранную тему "Различные способы решения систем линейных уравнений" является актуальной в связи с тем, что она систематизирует знания и позволяет учащимся лучше понять данную тему, т.к. способы решения систем линейных уравнений собраны в единое пособие.

В ходе работы над темой индивидуального проекта на тему "Различные способы решения систем линейных уравнений" реализована основная цель - знакомство с различными методами решения задач, основанными на материале программы по математике для 10 класса общеобразовательной средней школы, с задачами, имеющими нестандартный вид.

Системы линейных уравнений и задачи, содержащие более двух уравнений и более двух неизвестных, позволяют показать применение общих методов решения, а также расширить эти приемы специфическими, характерными для данного вида уравнений.

Находя новые приемы решения задач, при этом испытываешь радость и удовлетворение от самостоятельного решения.

1. Н.Я Виленкин, Г.С. Сурвилло и др. «Алгебра – 8», Учебное пособие для школ и классов с углубленным изучением математики, Новосибирск, ВО «Наука», 1992 г.
2. М.П. Галицкий, А.М. Гольдман, Л.И. Завич Сборник задач по алгебре для 8-9 классов. Учебное пособие для школ и классов с углубленным изучением математики, М., Просвещение, 1992 г., с. 117 - 119
3. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова «Высшая математика в упражнениях и задачах», том 1, Изд. Третье, М., «Высшая школа», 1980 г., с. 69 - 104
4. Е.Н. Ермолаева, З.Я. Квасникова, «Уравнения в курсе алгебры 8-10 классов средней школы», М., 1959 г., с. 66
5. И.С. Петраков «Математические кружки в 8-10 классах», М., Просвещение, 1987 г., с.13, 32, 82, 86