В процессе работы над индивидуальным проектом по математике "Теорема Пифагора" учеником 9 класса гимназии была поставлена и реализована цель рассмотреть практическое применения теоремы Пифагора в разных сферах деятельности человека и областях науки, помимо математики.

Подробнее о проекте:

В ученической исследовательской работе по математике "Теорема Пифагора" автор проводит анализ учебно-методической литературы и находит интересные сведения о Пифагоре. Также в проекте представлена правильная формулировка Теоремы Пифагора, приведено доказательство теоремы и представлены знаменитые философские высказывания Пифагора.

В готовом творческом и исследовательском проекте по математике "Теорема Пифагора" учащимся дано доказательство теоремы Пифагора через подобные треугольники, а также рассмотрено применение теоремы Пифагора в строительстве, в мобильной связи, в астрономии и в литературе. Школьник рассуждает над актуальностью применения теоремы Пифагора в повседневной жизни человека.

Оглавление

Введение
1. Это интересно знать.
2. Формулировка теоремы Пифагора.
3. Доказательство теоремы.
4. Философские высказывания Пифагора.
5. Доказательство теоремы Пифагора через подобные треугольники.
6. Применение теоремы Пифагора. Строительство.
7. Мобильная связь.
8. Астрономия.
9. Литература.
10. Применение теоремы Пифагора.
Выводы и заключение
Список литературы

На уроках геометрии мы познакомились с одной из важнейших теорем геометрии для прямоугольного треугольника, известной с древних времен – теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Кратко познакомились с историей этой теоремы, рассмотрели одно из ее доказательств, также узнали, что существуют и другие способы доказательства.

Трудно найти человека, для которого имя Пифагора не ассоциировалось бы с его теоремой. Почти у каждого сохранились воспоминания о «пифагоровых штанах» - квадрате на гипотенузе, равновеликом двум квадратам на катетах.

Причина такой популярности теоремы Пифагора очевидна: простота, красота и широкая значимость. Однако теорема Пифагора проста, но не так очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Кроме этого, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.) свидетельствует о гигантском числе ее конкретных реализаций. Зная теорему Пифагора, можно находить ее новые применения и способы доказательств.

С одной стороны – теорема Пифагора изучается и доказывается в школьном курсе геометрии, а с другой стороны - школьного материала явно недостаточно для того, чтобы показать ее практическую значимость в различных, в том числе и современных сферах деятельности человека.

Цель работы: Изучение практического применения теоремы Пифагора.

Задачи работы:

1. Изучение биографии Пифагора.
2. Изучение истории появления и развития теоремы Пифагора.
3. Рассмотрение доказательства теоремы Пифагора.
4. Подобрать интересные задачи, решаемые с помощью теоремы Пифагора.

Основные методы исследования: Метод исследования, систематизации и обработки данных.

Гипотеза: если теорема Пифагора так популярна и сегодня, то в ней заложены такие основы, которые позволяют использовать ее в различных, в том числе и современных сферах деятельности человека.

Объект исследования: практическое применение теоремы Пифагора в современной деятельности человека.

Предмет исследования: теорема Пифагора.

Пифагор родился (580-500 до н.э.) на острове Самос, одном из самых цветущих островов Ионии, в семье богатого ювелира. Он был очень красив и с детства отличался разумом и справедливостью. С юных лет Пифагор стремился проникнуть в тайны Вечной Природы, постичь смысл Бытия. Знания, полученные им в храмах Греции, не давали ответов на все волнующие его вопросы, и он отправился в поисках мудрости в Египет.

В течение 22 лет он проходил обучение в храмах Мемфиса и получил посвящение высшей степени. Здесь же он глубоко изучил математику, науку чисел или всемирных принципов, из которой впоследствии сделал центр своей системы. Кроме того, что Пифагор был математиком, он также имел отношение к литературе и философии.

Пифагора можно отнести и к великим мыслителям своего времени. Одна из самых главных заслуг Пифагора-это доказательство теоремы, которая носит его имя. Существует около 500 способов её доказательства, и это одна из теорем, которая доказывает большую часть математических теорем.

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника:

Сумма квадратов длин катетов равна квадрату длины гипотенузы.a²+b²=c²

Нужно знать зависимость между катетами и гипотенузой в прямоугольном треугольнике. Эту зависимость подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора.

Квадраты, построенные на катетах, состоят из 2-х  одинаковых треугольников. А квадрат, построенный на гипотенузе, состоит из 4-х таких треугольников. Вероятно, факт, изложенный в теореме Пифагора, сначала был дан для равнобедренных треугольников. Таким образом, площадь квадрата построенного на стороне С, равна сумме площадей квадратов, построенных на сторонах А и В.

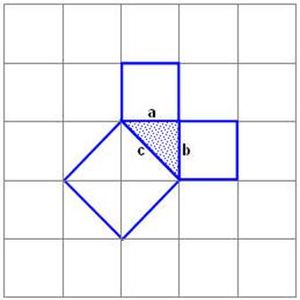
Доказательство теоремы

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. И в этом случае так же площадь квадрата построенного на гипотенузе С, будет равна сумме площадей квадратов, построенных на сторонах А и В.

Задача

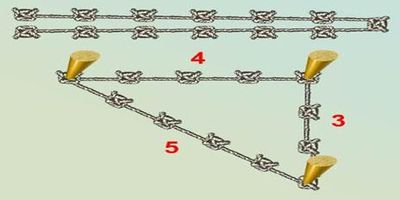
Древние египтяне для построения прямоугольных треугольников пользовались веревкой с завязанными на ней на одинаковых расстояниях узелками. По одной стороне они откладывали 3 отрезка, на другой 4, а на третьей 5.  Правильно ли они поступали?

Треугольник со сторонами 3, 4, 5 теперь  мы называем египетским.

1. Делай лишь то, что впоследствии не огорчит тебя и не заставит раскаиваться.
2. Статуя формой своей хороша, а человека украсят дела.
3. Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает.

Пусть треугольник ABC - прямоугольный треугольник с прямым углом C.

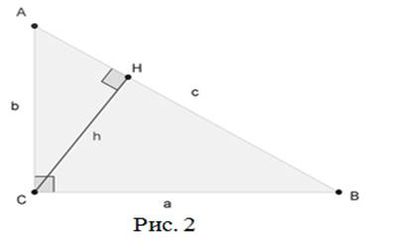
Проведём высоту из вершины C на гипотенузу AB, основание высоты обозначим как H.

Прямоугольный треугольник ACH подобен треугольнику ABC по двум углам (∠ACB=∠CHA=90%, ∠A- общий). Аналогично, треугольник CBH подобен ABC.

Введя обозначения

BC=a, AC=b, AB=c

из подобия треугольников получаем, что

a/c=H/B, b/c=A/H

Отсюда имеем, что

a2=c⋅HB,  b2=c⋅AH

Сложив полученные равенства, получаем

a2+b2=c⋅HB+c⋅AH

a2+b2=c⋅(HB+AH)

a2+b2=c⋅AB

a2+b2=c⋅c

a2+b2=c2

Что и требовалось доказать.

Задача 1

От столба высотой 9 м к дому натянут провод, который крепится на высоте

3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.

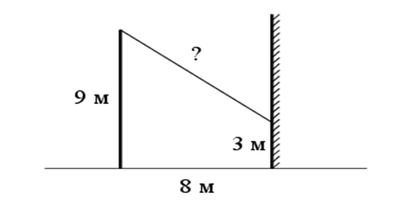
Решение задачи

Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD - прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD.

По теореме Пифагора

BC2=CE2+EB2

BC2=82 + (9-3)2

BC2=64+36

BC2=100  

BC=10.

Ответ:10.

Задача 2

Длина стремянки в сложенном виде равна 1,85 м, а её высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.

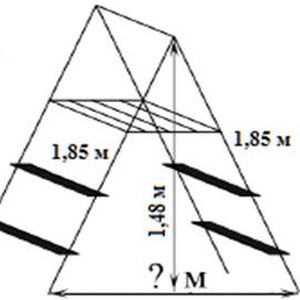
Решение задачи

Данная задача сводится к нахождению катета прямоугольного треугольника. Пусть х — искомое расстояние, тогда:

Ответ: 2,22.

Задача 3

Девочка прошла от дома по направлению на запад 880 м. Затем повернула на север и прошла 900 м. После этого она повернула на восток и прошла ещё 400 м. На каком расстоянии (в метрах) от дома оказалась девочка?

Решение задачи

Восток и запад — противоположные направления, поэтому девочка прошла 880 − 400 = 480 м на запад. Пусть  — гипотенуза прямоугольного треугольника. По теореме Пифагора, гипотенуза ищется следующим образом:

Ответ: 1020.

Задача 5

Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)

Решение задачи

Пусть AB=x, BC=R=200 км, OC=r=6380 км.

OB=OA+AB

OB= r + x.

Используя теорему Пифагора, получим 23 км

Ответ: 23 км.

Задача 6

На этом рисунке показаны точки A и B и путь светового луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч - прямой. Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равно расстояние между точками?

Решение задачи

На этом рисунке показан путь светового луча только с другой точки зрения, например из космического корабля. Предположим, что корабль движется влево. Тогда две точки, между которыми движется световой луч, станут двигаться вправо с той же скоростью.Причем, в то время, пока луч пробегает свой путь, исходная точка A смещается, и луч возвращается уже в новую точку C.

Вконце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремыПифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Теорема Пифагора вдохновляла писателей со времен античности и продолжает это делать в наше время. Например, немецкого писателя девятнадцатого века Адельберта фон Шамиссо она вдохновила на написание сонета:

В 20 веке советский писатель Евгений Велтистов в книге «Приключения Электроника» доказательствам теоремы Пифагора отвел целую главу! И еще полглавы рассказу о двухмерном мире, какой мог бы существовать, если бы теорема Пифагора стала основополагающим законом и даже религией для отдельно взятого мира. Жить в нем было бы гораздо проще, но и гораздо скучнее: например, там никто не понимает значения слов «круглый» и «пушистый».

В книге «Приключения Электроника» автор устами учителя математики Таратара говорит: «Главное в математике – движение мысли, новые идеи». Именно этот творческий полет мысли порождает теорема Пифагора – не зря у нее столько разнообразных доказательств. Она помогает выйти за границы привычного, и на знакомые вещи посмотреть по-новому.

Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдём: Катеты в квадрат возводим, Сумму степеней находим И таким простым путём К результату мы придём.

Успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов, которые позволяют решать задачи, выдвигаемые практикой. Теорема Пифагора применяется в строительстве, астрономии, мобильной связи, литературе  и т.д.

В научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).

Теорема Пифагора - одна из главных и, можно сказать, самая главная теорема геометрии. Теорема Пифагора триедина: это простота – красота – значимость. Мы познакомились с некоторыми доказательствами теоремы Пифагора.

Есть доказательства, которые рассчитаны на то, что по готовым рисункам, можно воспроизвести доказательство самостоятельно. А это воспитывает познавательный интерес и логическое мышление. До сих пор вызывают интерес древние практические задачи, говорящие об уровне развития прикладной математики в древние века.

1. Атанасян Л.С. и др. «Геометрия 7-9», М. «Просвещение»,2002г.
2. Погорелов А.В.«Геометрия 7-11», М.«Просвещение»1992г.
3. Волошинов А.В. «Пифагор», М. «Просвещение», 1993г.
4. Литцман В. «Теорема Пифагора»,М. «Государственное издательство физико-математической литературы», 1960г.
5. Руденко В.Н. «Геометрия 7-9», М. «Просвещение»1992г.
6. Еленьский Щ. По следам Пифагора М. 1961г.