Проект "Оленьи рога на языке геометрии"

В ходе исследовательского проекта по математике (геометрия) на тему "Оленьи рога на языке геометрии" учащийся 8 класса выяснил, что существуют четко определенные геометрические преобразования одного элемента для описания в полной мере ненецкого орнамента «Оленьи рога», но порядок проведения этих построений может быть разным.
Подробнее о проекте:
В исследовательской работе по математике (геометрии) "Оленьи рога на языке геометрии" ученик изучает научную литературу по теме исследования, а также ученические проекты на аналогичные темы, выясняет, что среди опубликованных работ обучающихся нет таких, которые описывают построение ненецкого орнамента «Оленьи рога» через определенные геометрические преобразования.
Помимо изучения литературы автор в своем исследовательском проекте по математике (геометрии) об орнаменте "оленьи рога" рассмотрел виды и типы орнаментов, изучил виды преобразований плоскостных фигур, применил знания на практике, создав последовательность геометрических преобразований ненецкого орнамента «Оленьи рога».
Оглавление
Введение
1. Виды и типы орнаментов народов Ямало-Ненецкого автономного округа.
2. Геометрические преобразования.
3. Орнамент «Оленьи рога» на языке геометрии.
Заключение
Список используемой литературы
Приложения
Введение
Цель исследовательской работы: Определить геометрические преобразования и их последовательность для создания ненецкого орнамента - «Оленьи рога».
При написании работы были использованы следующие методы научного исследования:
- анализ литературы и материалов сети Internet;
- синтез;
- опрос-анкетирование,
- статистический метод при обработке информации;
- моделирование;
- обобщение, сравнение;
- вывод.
Мы выяснили, что интерес к орнаменту актуален в современном мире, что все обучающиеся 8 класса знают орнамент «Оленьи рога», который используется на флаге и гербе Ямало-Ненецкого автономного округа.
Оказывается, все многообразие орнаментов имеет свою классификацию. А рассматриваемый нами орнамент является геометрическим ленточным.
Кроме этого мы определили, что в настоящее время принятой общей системы обозначения, подобной языку алгебры в геометрии, которая позволяла бы точно и компактно описывать алгоритмы решения конструктивных задач (задач на построение), не существует. Поэтому нам пришлось договариваться об обозначениях преобразований.
Исследования позволяют сделать вывод о том, что существуют четко определенные геометрические преобразования одного элемента для описания в полной мере ненецкого орнамента «Оленьи рога». Но порядок проведения этих построений может быть разным. Таким образом, высказанная нами гипотеза в части четко определенного порядка геометрических преобразований одного элемента для описания в полной мере ненецкого орнамента «Оленьи рога» не подтвердилась.
Мы сумели получить интересный материал, который демонстрирует межпредметные связи и дает возможность людям, которые не обладают талантом художника, создавать красоту, опираясь на знания геометрии.
Человек с древних времен стремится окружить себя и пространство чем-то красивым, приятным глазу. Для украшения различных предметов: одежды, обуви, посуды, предметов интерьера, оружия и даже архитектурных сооружений используют орнамент. Красота орнаментов рукотворна. Однако важное место в орнаментальном искусстве занимают геометрические знания и умения мастера.[6]
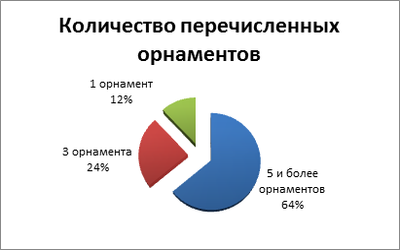
Проведенный опрос среди одноклассников показал, что 64% обучающихся знают 5 и более ненецких орнаментов, 24% назвали по 3 орнамента, остальные 12% помнят название одного из орнаментов. Среди ответов чаще всего встречался орнамент - «Оленьи рога».
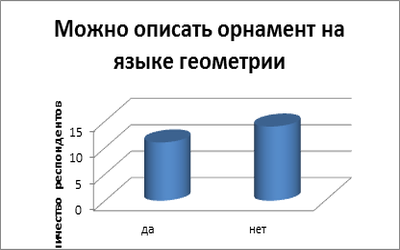
Следует отметить, что возможность в полной мере описать орнамент на языке геометрии признали почти половина респондентов (Приложение № 1). Кроме этого флаг и герб Ямало-Ненецкого автономного округа содержат орнамент «Оленьи рога». Среди современных учёных данным вопросом занимался в частности Жеребцов Андрей Николаевич, кандидат технических наук, который в 2008 году написал диссертацию «Дизайн двумерных орнаментов».
Таким образом, интерес к орнаменту актуален и сегодня.
Все вышесказанное и обусловило выбор темы исследовательской работы: «Оленьи рога на языке геометрии».
Работая над темой, мы сталкивались с работами, в которых описаны пошаговые схемы вычерчивания орнамента на клеточной бумаге. Мы же в своей работе представим орнамент «Оленьи рога» через геометрические преобразования.
Проблема исследования: Какой последовательностью геометрических преобразований базовых элементов в полной мере можно описать ненецкий орнамент «Оленьи рога»?
Цель: Определить геометрические преобразования базовых элементов и их последовательность для создания ненецкого орнамента - «Оленьи рога».
Для достижения поставленной цели нам необходимо решить следующие задачи:
- Проанализировать доступную информацию по теме;
- Рассмотреть виды и типы орнаментов;
- Изучить виды преобразований плоскостных фигур;
- Применить знания на практике, создав последовательность геометрических преобразований ненецкого орнамента «Оленьи рога».
- Сформулировать выводы.
Объект исследования: ненецкий орнамент «Оленьи рога».
Предмет исследования: геометрические преобразования базовых элементов ненецкого орнамента.
Гипотеза исследования: Существует четко определенный порядок геометрических преобразований базовых элементов для описания в полной мере ненецкого орнамента «Оленьи рога».
При написании работы были использованы следующие методы научного исследования:
- анализ литературы и материалов сети Internet;
- синтез;
- анкетирование;
- статистический метод при обработке информации;
- моделирование;
- обобщение, сравнение;
- вывод.
Основные этапы исследования:
І этап. Подготовка к исследовательской работе.
ІІ этап. Планирование исследовательской работы.
ІІІ этап. Исследование.
V этап. Выводы.
VI этап. Оформление работы.
VІI этап. Отчет и защита исследовательской работы.
Практическая значимость работы заключается в том, что мы сумели получить интересный материал, который демонстрирует межпредметные связи и дает возможность людям, которые не обладают талантом художника, создавать красивые орнаменты, опираясь на знания геометрии.
Работа состоит из оглавления; введения, где определена цель исследования, методы исследования, гипотеза и т.д.; основной части, состоящей из трёх глав, заключения, где сформулированы выводы и результаты; списка литературы и приложения.
Виды и типы орнаментов народов Ямало-Ненецкого автономного округа
Орнамент — узор, основанный на повторе и чередовании составляющих его элементов; предназначается для украшения различных предметов.[4]
Поэтому нам необходимо рассмотреть понятие «раппопорта».
Rapport, от rapporter — приносить обратно — базовый элемент орнамента, часть узора, повторяющаяся многократно в художественном оформлении ткани (включая трикотаж, вышивку, ковры) и в других областях прикладного искусства — на обоях, в иллюстрациях и т. п. Орнаменты разных народов мира индивидуальны они различаются особенностями восприятия окружающей среды и предметов.[6]
Орнаменты народов ЯНАО основаны на прямом восприятии природы. Как пишет Г. Сусой: «…на орнаментах, геометрически точно вырезанных, изображена вся тундра, с реками, озерами, с глазами, копытами и ушками оленя, следами других животных, птиц и зверей» пишет.[3]
Исследователи делят орнаменты на следующие виды:
- геометрический орнамент – состоит из геометрических элементов, характерно строгое чередование элементов и их цветовое сочетание.
- растительный орнамент – состоит из растительных элементов, которые могут отличаться от природных растительных форм, например: цветы или листья изображаются в продольном разрезе, развернутыми в фас.
- зооморфный орнамент – в основу положены как реалистические, так и условные, стилизованные изображения птиц, зверей, рыб.
- антропоморфный - декор, в котором используются повторяющиеся изображения женских и мужских стилизованных фигур либо лиц [5] (Приложение № 2).
По расположению и характеру композиции, орнамент бывает:
- ленточным — в виде прямой или криволинейной орнаментальной полосы, которая украшает середину изделия или окаймляет его (фриз, бордюр);
- сетчатым, при котором вся поверхность заполнена узором;
- центрическим, или розеточным, в котором отдельные элементы орнамента вписаны в квадрат, круг, ромб или многоугольник (т.е. розетку), расположенный в центре [5]: (Приложение № 3).
Внимательно рассмотрев ненецкий орнамент «Оленьи рога» (Приложение № 4), становится очевидным, что он является геометрическим ленточным орнаментом.
Геометрические преобразования
Очень часто, сами не подозревая того, мы имеем дело с геометрией. Мы вовлекаемся в геометрию, когда работаем с формой и размерами, предметами, их размещением в пространстве.
Как отмечает Д. Гильберт: «В настоящее время принятой общей системы обозначения, подобной языку алгебры в аналитической геометрии, которая позволяла бы точно и компактно описывать алгоритмы решения конструктивных задач (задач на построение), не существует.[7]
Так или иначе, наиболее распространенной формой представления алгоритмов решения конструктивных задач остается чертеж, дополненный словесным описанием или геометрическими формулами принадлежности, параллельности, перпендикулярности и теоретико-множественными операциями. В результате — геометрические алгоритмы до сих пор остаются «более громоздки и трудоёмки, чем аналитические».[2]
Рассмотрев весь перечень видов преобразований (Приложение № 5), и, учитывая особенности орнамента «Оленьи рога», из всего перечня преобразований, будем использовать:
- параллельный перенос,
- преобразование симметрии относительно точки или прямой.
В математике используются символы для упрощения и сокращения текста. И мы договоримся об обозначениях этих преобразований.
| N п/п | Название преобразования | Обозначения |
| 1 | Симметрия относительно прямой L | SL: L – ось симметрии |
| 2 | Параллельный перенос | Ta→, Tфигуры – перенос на вектор a |
| 3 |
В результате мы поняли, что геометрия – это не только задачи на построение, счёт, цифры, но и уникальное средство познания красоты.
Орнамент «Оленьи рога» на языке геометрии
Теперь мы выявили структуру и композиционные особенности составляющих элементов орнамента «Оленьи рога».
За элементы орнамента, на основе которых будем описывать «Оленьи рога» примем равнобедренный треугольник и ромб.
Тогда, орнамент «Оленьи рога» на языке геометрии будет иметь вид представленный в Приложении № 6.
Повторять необходимое количество раз для завершения орнамента, который наносится на одежду, предметы утвари и т.д. (Приложение № 7).
Действия с базовой фигурой – треугольник условимся проводить по порядку, учитывая очерёдность осей симметрии.
Выстраивание фигуры из 10 ромбов, как оказалось, можно проводить, изменяя очередность определения местоположения базовой фигуры и очередности заполнения вакантных мест (Приложение № 8). Таких возможных вариантов получается 17 310 309 456 440 штук.
Таким образом, мы пришли к следующему выводу: можно четко определить перечень геометрических преобразований, но порядок этих преобразований может быть любым, то есть при любой последовательности построений мы получим исходный орнамент «Оленьи рога».
Заключение
Работая над темой, мы узнали много нового и интересного. В результате работы научились: подбирать нужный теоретический материал, относится критически к полученной информации, искать способы для подтверждения или опровержения, подбирать нужные иллюстрации и делать выводы по результатам. Кроме этого нам пришлось изучить понятие параллельного переноса, которое рассматривается только в 9 классе. Всё это не просто и требует много времени, но очень интересно.
Мы выяснили, что интерес к орнаменту актуален в современном мире, что все обучающиеся 8 класса знают орнамент «Оленьи рога», который используется на флаге и гербе Ямало-Ненецкого автономного округа.
Оказывается, все многообразие орнаментов имеет свою классификацию. А рассматриваемый нами орнамент является геометрическим ленточным.
Кроме этого мы определили, что в настоящее время принятой общей системы обозначения, подобной языку алгебры в геометрии, которая позволяла бы точно и компактно описывать алгоритмы решения конструктивных задач (задач на построение), не существует. Поэтому нам пришлось договариваться об обозначениях преобразований.
Наша исследовательская работа позволяет сделать вывод о том, что существуют четко определенные геометрические преобразования базовых элементов для описания в полной мере ненецкого орнамента «Оленьи рога». Но порядок проведения этих построений может быть разным. Таким образом, высказанная нами гипотеза в части четко определенного порядка геометрических преобразований базовых элементов для описания в полной мере ненецкого орнамента «Оленьи рога» не подтвердилась.
Новизна работы заключается в том, что среди опубликованных работ обучающихся нет работ, которые описывают построение ненецкого орнамента «Оленьи рога» через определенные геометрические преобразования, конкретных базовых фигур.
Возможности геометрических преобразований в объяснении построения орнаментов не исчерпаны. Они бесконечны и интересны. Это ведёт к пониманию и более глубокому осмыслению геометрии, как прикладной науке о красоте. Если, например, взять один базовый элемент – треугольник, то результат работы будет другим.
«Красота тесно связана с симметрией», сказал Г. Вейль, а мы позволим себе добавить: «…и с параллельным переносом».[1]
Проблема нашего исследования заключается в том, какой последовательностью геометрических преобразований базовых элементов в полной мере можно описать ненецкий орнамент «Оленьи рога». Исходя из этого, мы выдвинули гипотезу: существует четко определенный порядок геометрических преобразований базовых элементов для описания в полной мере ненецкого орнамента «Оленьи рога».
Для исследования данной темы мы использовали следующие методы научного исследования: анализ литературы и материалов сети Internet; синтез, анкетирование, статистический метод при обработке информации, моделирование, обобщение, сравнение, вывод.
При анализе литературы, а особенно материалов сети Internet, так же встречались любопытные факты, которые вызывали интерес и желание углубиться в данную тему.
В нашей работе ключевой метод - это моделирование. Он помог нам сделать определённые выводы, которые не всегда оказывались предсказуемыми. Благодаря этому моделировать было очень интересно и познавательно.
Анкетирование, которое мы провели среди одноклассников, показал нам, что данная тема будет полезна школьникам, а так же помогло определится к конкретным орнаментом для изучения.
Работа состоит из оглавления; введения, где определена цель исследования, методы исследования, гипотеза и т.д.; основной части, состоящей из трёх глав, заключения, где сформулированы выводы и результаты; списка литературы и приложений.
Список используемой литературы
- Глейзер Г. И., История математики в школе⁄ Г. И. Глейзер ⁄⁄ История математики в школе: пособие для учителей/под редакцией В. Н. Молодшего. – М.: Просвещение, 1964. – С97
- Гильберт Д., Кон-Фоссен С. Наглядная геометрия. – М.: Наука,1981. – С344
- Сусой Е.Г. «Из глубины веков»//: Изд-во Том, 1994 - С228
- Энциклопедический словарь юного математика / cост. Савин А.П. – М. Просвещение, 1986.- С135
Приложение №1
Приложение №2
Виды орнаментов
| N п\п | Наименование | Пример изображения |
| 1 | Геометрический |

|
| 2 | Растительный |

|
| 3 | Зооморфный |

|
| 4 | Антропоморфный |

|
Приложение № 3
Виды орнаментов по расположению и характеру композиции
| N п\п | Наименование | Пример изображения |
| 1 | Ленточный |

|
| 2 | Сетчатый |

|
| 3 | Центрический |

|
Приложение № 4

Приложение № 5

Приложение № 7

Приложение № 8
| Возможные варианты | Геометрическое построение |
|
Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: Ckn=n!/((n−k)!⋅k!). В нашем случае С10010=17310309456440 возможных вариантов построения раппопорта орнамента |
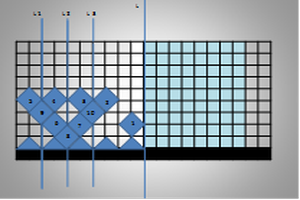 17310309456440 вариантов |
