В исследовательском проекте по математике (геометрия) на тему "Глубина залегания станций Новосибирского метрополитена" учащаяся 8 класса пытается узнать, какова средняя глубина станций Новосибирского метро и как узнать примерную глубину заложения станции. В исследовательской работе автор выясняет, как устройство эскалатора, прямоугольный треугольник и тригонометрические функции могут помочь в выполнении задач проекта.

Подробнее о проекте:

В ходе исследовательской работы по математике (геометрии) "Глубина залегания станций Новосибирского метрополитена" ученица изучает научную литературу по теме исследования, выясняет, какие теоретические знания необходимы для исследования, выполняет необходимые измерения и собирает данные на станциях метро Новосибирска, а также проводит математические расчеты для определения глубины заложения станции метро.

Помимо изучения литературы автор в своем исследовательском проекте по математике (геометрии) о глубине залегания станций Новосибирского метрополитена фотографирует необходимые части станций «Октябрьская» и «Сибирская», подсчитывает и измеряет необходимые длины и части на станциях Новосибирского метрополитена «Октябрьская» и «Сибирская» и в итоге проводит обработку и анализ полученных данных.

Оглавление

Введение
1. Подготовка к исследованию.
1.1 Научные и исторические сведения.
1.2 Сбор информации.
2. Проведение исследования.
2.1 Первый этап исследования.
2.2 Второй этап исследования.
Заключение
Список литературы

А вам интересно, какова средняя глубина станций Новосибирского метро?
А как узнать примерную глубину заложения станции? Попробуем найти ответ!

Актуальность: в современном информационном пространстве можно найти ответ на любой вопрос, но можем ли мы самостоятельно, применяя знания школьного курса геометрии, ответить на вопрос: «На какой глубине расположены станции Новосибирского метрополитена».

Объект исследования: станции Новосибирского метрополитена.

Предмет исследования: глубина заложения станций Новосибирского метрополитена.

Цель: определить глубину заложения станций Новосибирского метрополитена, применяя знания школьного курса геометрии.

Задачи исследовательской работы:

• изучить научную литературу по теме моего исследования;
• определить, какие теоретические знания необходимы для исследования;
• выполнить необходимые измерения и сбор данных на станциях метро;
• выполнить необходимые расчеты для определения глубины заложения.

Гипотеза: Как устройство эскалатора, прямоугольный треугольник и тригонометрические функции могут мне помочь в моей исследовательской работе.

Методы исследования:

• Изучение литературы и других источников информации.
• Наблюдение.
• Фотографирование необходимых частей станции «Октябрьская» и «Сибирская».
• Счет и измерение необходимых длин и частей на станции «Октябрьская» и «Сибирская».
• Обработка полученных данных.

Теоретическая значимость моей работы заключается в том, что благодаря знаниям в области геометрии можно решать многие трудные задачи.

Практическая значимость моей работы заключается в том, что с этой работой я могу принять участие в «Научно - практической конференции» в моей школе и применять полученные знания в новой ситуации.

План работы:

1. Изучить научную литературу по теме моего исследования.

2. Определить количество фонарей на эскалаторе на станциях «Октябрьская» и «Сибирская».

3. Проанализировав полученные результаты и воспользовавшись формулами из геометрии выявить глубину заложения станций Новосибирского метрополитена.

1. Подготовка к исследованию

1.1 Научные и исторические сведения

Немного истории. Первая линия метро была открыта в Лондоне еще в 1836 году. Ее строительством занималась компания под названием Metropolitan Railways. Это словосочетание можно перевести как «Столичные железные дороги». Но именно от этого слова образовалось название нового вида транспорта во многих странах. Первоначально лондонское метро работало на паровой тяге. В 1890 году оно было электрифицировано.

Следующим использовать метро стал Нью-Йорк. В 1868 г. здесь было открыто несколько наземных станций. Первая подземная линия в этом городе открылась через 36 лет. Следующим стал использовать новый вид транспорта Чикаго. Метрополитен здесь открылся в 1892 году. Несколько отстала в этом вопросе Россия. Метро здесь впервые появилось в 1935 году, в Москве. И только через 20 лет – в Санкт-Петербурге.

На сегодняшний день самой протяженной остается Нью-йоркская подземка. Она включает 26 линии и ежегодно перевозит 1,6 миллиарда человек. Но шанхайский метрополитен является самым динамично развивающимся. К 2025 году планируется построить 21 дополнительную линию. Пассажиропоток за сутки составляет 5 миллионов человек.

Самые глубокие в мире Первое место по этому параметру - за украинской станцией «Арсенал». Ее глубина составляет 105,5 метров. Она была запущена 6 сентября 1960 года. Первоначально ее украшал барельеф, посвященный работникам одноименного завода, но после обретения Украиной независимости его демонтировали. Второе занимает российская «Адмиралтейская» с глубиной в 86 метров. Она была запущена в эксплуатацию 28 декабря 2011 года. Интересно, что она была практически закончена уже в 1997 г., но из-за проблем с инженерными работами строительство было продолжено только через 10 лет.

Третье место за корейской станцией «Пухунг». Она была построена в 1987 году. В ее оформлении используются мраморные изображения лидеров КНДР. Это одна из двух станций Пхеньяна, куда проводятся экскурсии для туристов. Четвертое место за «Парком Победы» в Москве. Станция оформлена в стиле Великой Отечественной войны. Наконец, на пятом месте расположилась самая глубокая станция США – «Вашингтон Парк» портлендского метро. Она была запущена в эксплуатацию в 1998 году.

Глубина московского метро – 24 метра.

28 декабря 1985 года в эксплуатацию был введен новосибирский метрополитен.

Как оценить глубину заложения станции метро, на которую вы спускаетесь по эскалатору? Оказывается и в этом житейском вопросе может помочь знание математики! А именно — тригонометрии.

Тригономе́трия (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю», то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии[1]. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии (науке, исследующей размеры и форму Земли).

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии во многих областях науки и техники.

«Эскалатор метро... Как много в этих словах скрыто для любого интересующегося человека! Огромная, постоянно движущаяся махина, «живая лестница»...

А начиналось всё ещё в конце XIX века, когда американский изобретатель Дж. Рено (Jesse W. Reno, 1861—1947) запатентовал первую «живую лестницу». В его конструкции вместо ступенек на «бесконечной» ленте её лестничного полотна были продольные рифли. Первый же публичный действующий эскалатор по соглашению с его изобретателем Ч. Зеебергером (Charles D. Seeberger, 1857—1931) был изготовлен компанией «Отис» и экспонирован на Парижской выставке 1900 года. У него были горизонтальные ступени, которые выходили из-под ограждения на одной входной площадке и уходили под такое же ограждение на другой входной площадке, что доставляло массу проблем. В 1921 году обе идеи — горизонтальные ступеньки и рифление — были объединены в новой конструкции, и с этого момента всегда стала использоваться подобная схема.

Когда в 1930-х годах начали проектировать первый в нашей стране московский метрополитен, была предпринята попытка ознакомиться с заграничным опытом. Однако запрашиваемые суммы и время на исполнение со стороны зарубежных компаний были настолько велики, что от этой идеи пришлось отказаться. В конце 1933 года директор лондонского отделения фирмы «Отис» писал председателю Моссовета: «Ваши специалисты — способный народ. Но эскалаторы — чрезвычайно сложное дело, им с этим делом не справиться. Даже мы, с нашим тридцатилетним опытом, не возьмёмся выполнить заказ в такие сроки. Я, как друг Советского Союза, обязан вас предупредить, что сроки пуска метро могут быть сорваны». Но советские инженеры и учёные сумели решить эту уникальную задачу, и в феврале 1935 года эскалаторы стали доставлять пассажиров на станции московского метрополитена

Одним из важных элементов эскалатора является ступенька.

У неё четыре ролика: два больших и два маленьких. Большие ролики едут по своим направляющим рельсам, а маленькие — по своим.

Когда проектировали эскалатор, даже подбор материалов для роликов был очень важной и трудной задачей. Московский метрополитен открыт примерно с шести утра до часу ночи. Т. е. больше 19 часов — больше 68 тысяч секунд в день. Самая медленная скорость эксплуатации эскалатора сейчас 0,75 м/c, и, значит, ступенька пробегает каждый день больше 50 километров. И так, без устали, день за днём, в год более 18 тысяч километров! Представляете, каков должен быть материал, чтобы ролики без регулярных ремонтов и замен могли выдерживать постоянно едущих на ступеньках пассажиров. И это только одна деталь и один вопрос, который пришлось решать советским инженерам, а таких вопросов были тысячи.

Вот так примерно выглядит схема эскалатора.

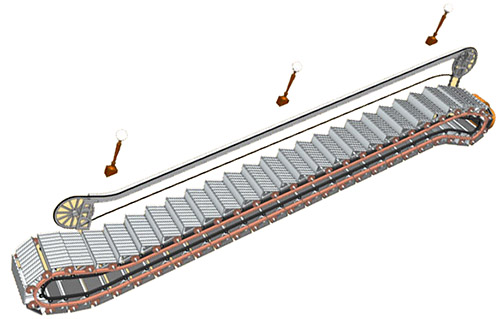
Если посмотреть сбоку, то видно, что именно взаимное расположение направляющих рельс больших и маленьких роликов обеспечивает основное свойство эскалатора: в верхней части «живой лестницы», по которой едут пассажиры, ступени всегда горизонтальны. В нижней же части ступени возвращаются вверх параллельно направляющим, не занимая место в туннеле.

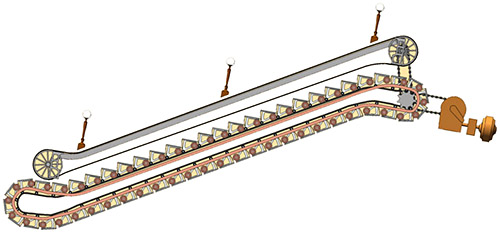
Но вернёмся к нашему вопросу о глубине, на которую спускается эскалатор. Удивительный факт состоит в том, что все российские эскалаторы, с самых первых и до производимых в наше время, наклонены к горизонту под углом в 30 градусов!

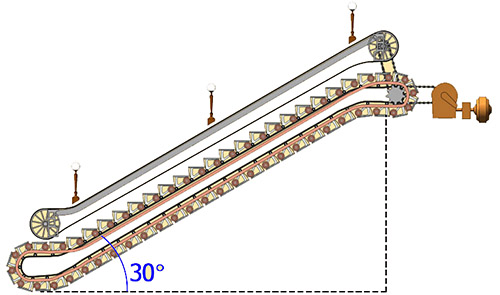
Достроим мысленно эскалатор до естественного прямоугольного треугольника. Длина его гипотенузы — это длина эскалатора, а длина одного из катетов и будет примерно равна глубине заложения той станции метро, на которую ведёт этот эскалатор.

Как же посчитать длину эскалатора, спускаясь по нему? Можно было бы засечь время, но тогда для вычисления пути нужно точно знать скорость движения, а она может меняться от 0,75 м/c до 1 м/c, и погрешность — в четверть — довольно большая.

Можно было бы посчитать размеры одной ступеньки, но затем понять на движущемся эскалаторе, сколько на гипотенузе умещается ступенек, сложновато...

Что же мы можем использовать ещё? Спускаясь или поднимаясь по эскалатору, мы постоянно проезжаем фонари! Расстояние между ними не фиксируется, ГОСТами оговаривается необходимая освещённость туннеля. И в итоге получается, что фонари отстоят друг от друга примерно на 5 метров.

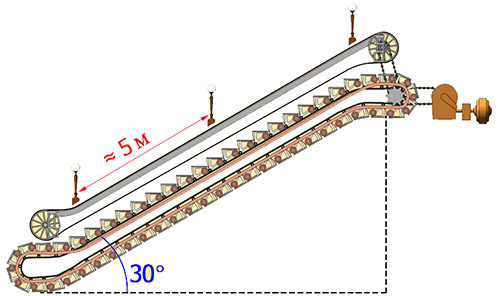
Спускаясь по эскалатору, можно посчитать количество фонарей.

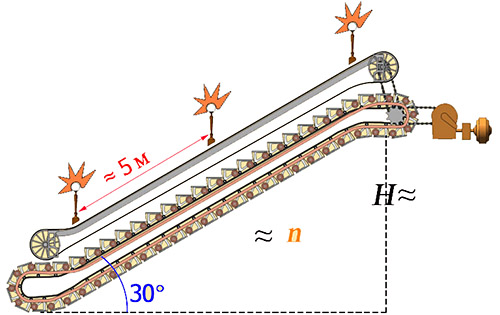
Что нужно сделать дальше, чтобы посчитать длину гипотенузы?

Не торопитесь умножать на 5. Для подсчёта длины нам же нужно не количество фонарей, а количество расстояний между ними! От подсчитанного количества фонарей следует отнять 1, а теперь уже можно умножать на 5 и на синус 30°.

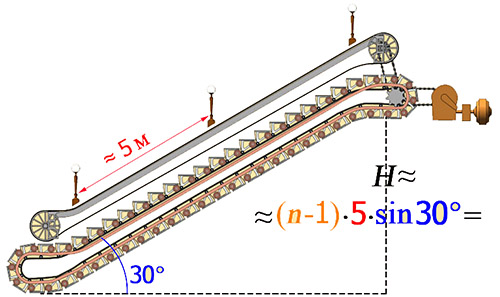
Красота момента состоит в том, что синус 30° равен 1/2, и с этим числом легко производить счёт в уме! И получившаяся формула подсчёта глубины заложения станции проста для счёта и легка для запоминания.

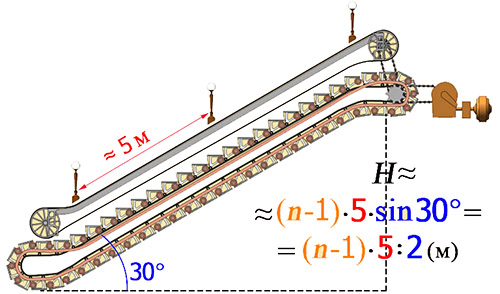
Впрочем, эту формулу можно написать и не зная «синусов» — о том, что катет прямоугольного треугольника, противолежащий углу в 30°, равен половине гипотенузы, школьники узнают ещё до изучения тригонометрии.» Глубина заложения станций метрополитена // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — М.: Математические этюды, 2015. — С. 47.

1.2 Сбор информации

Станция «Октябрьская» Ленинская линия Новосибирский метрополитен.

Дата открытия 7 января 1986.
Тип колонная трёхпролётная мелкого заложения.
Глубина заложения, м 11.
Длина платформы, м 102.
Ширина платформы, м 10.
Архитекторы Питерский В. В., Нечаева Л., Барановская И. А.
Инженеры‑конструкторы Кожевников В. Н.

Станция «Сибирская» Дзержинская линия Новосибирский метрополитен.

Дата открытия 31 декабря 1987 года
Проектное название «Нарымская»
Проекты переименования "Центральная" (1992 год)
Тип колонная трёхпролётная мелкого заложения
Глубина заложения, м 16
Длина платформы, м 102
Ширина платформы, м 10
Архитекторы Питерский В.В
Художники Алексеев Г.Л. и Алексеева О.М.
Инженеры‑конструкторы Романов В.И

2. Проведение исследования

2.1 Первый этап исследования

«Глубина заложения Новосибирской станции метро «Октябрьская»

На станции «Октябрьская» 5 фонарей на эскалаторе, значит его глубина заложения на станции, равна 10м.

Вычисляем по формуле (5-1)∙5∙0,5 ≈10 м .

На сайте Новосибирского метрополитена указана глубина заложения 11 м.

2.2 Второй этап исследования

«Глубина заложения Новосибирской станции метро «Сибирская».

На станции «Сибирская»7 фонаря на эскалаторе, значит его глубина заложения на станции, равна 15 метров.

Вычисляем по формуле (7-1)∙5∙0,5≈15 м.

На сайте Новосибирского метрополитена указана глубина заложения 16 м.

Вывод: Изучая научную литературу, я узнала, что средняя глубина заложения станций 9 м., а самая глубокая станция – это станция «Сибирская».

Заключение

В ходе работы над исследовательским проектом по математике на тему "Глубина залегания станций Новосибирского метрополитена" я выяснила, как знание геометрии могут помочь в решении трудных задач.

Я узнала, с помощью какой формулы, можно определить глубину заложения метрополитена. И благодаря помощи моего одноклассника и учителя смогла найти глубину заложения станций «Октябрьская» и «Сибирская» Новосибирского метрополитена. Теперь, находясь в метро любой страны, я смогу оценить глубину заложения станций.

Литература

Л.А. Островский. Живая лестница // Как мы строили метро. М., 1935.

Лестница-чудесница // Московскому метрополитену — 50. М., 1985

Глубина заложения станций метрополитена // Математическая составляющая / Ред.-сост. Н.Н. Андреев, С.П. Коновалов, Н.М. Панюнин. — М. : Математические этюды, 2015. — С. 47.