Приложение 1. О чем надо помнить решая квадратные уравнения?

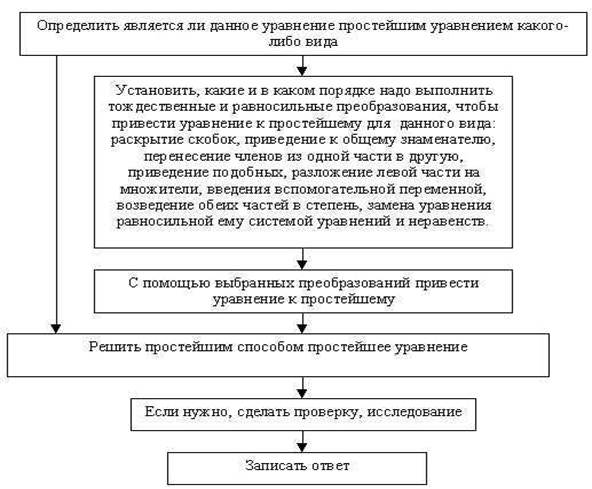
Приём контроля решения уравнения алгебраическим способом

1. Проверить, правильно ли определён вид уравнения.

2. Проверить, приводят ли данное уравнение к простейшему выбранные тождественные и равносильные преобразования.

3. Проверить правильность выполнения преобразований.

4. Проверить применение правила (формулы, алгоритма) решения простейшего уравнения.

5. Проверить вычисления при проверке решения.

6. Проверить запись ответа.

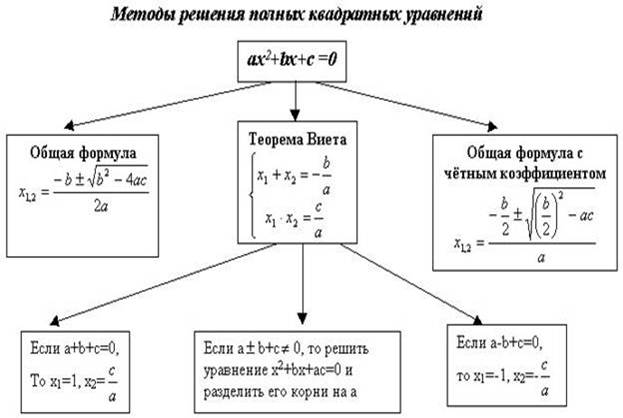
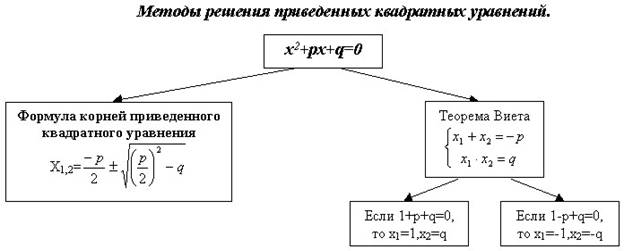
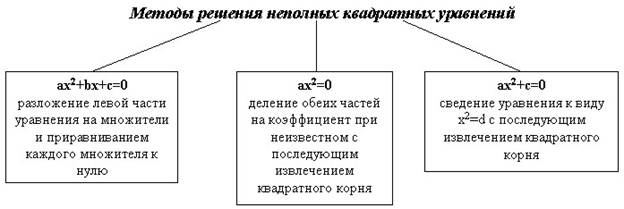
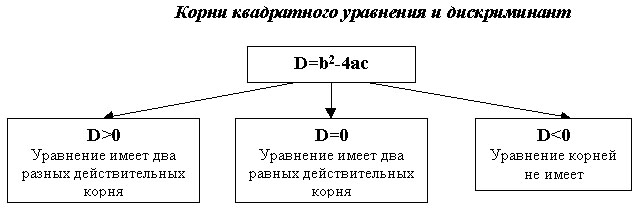
Приложение 2. Дидактический материал по применению нестандартных приемов решения квадратных уравнений

1. Найди наиболее рациональным способом корни уравнения:

а) 4х2 – 13х + 9 =0 (1; 2,25)

б)1978х2 – 1984х + 6=0 (1; 6/1978)

в) 4х2 + 11х + 7 = 0 (-1; -7/4)

г) 319х2 + 1988х +1669=0 (-1; -1669/319)

д) 1999х2 + 2000х+1=0 (-1; -1/1999)

2. Решить квадратные уравнения с большими коэффициентами

а) 313х2 +326х+13=0 (-1; -13/313)

б) 839х2– 448х -391=0 (1; -391/839)

в) 345х2 – 137х – 208=0 (1;.-208/345)

г) 939х2+978х+39=0 (-1; -39/939)

3. Используя полученные знания, установи соответствие:

1) х2+5х+6=0 2) 6х2-5х+1=0 3) 2х2-5х+3=0 4) 3х2-5х+2=0 5) х2-5х+6=0 6) 6х2+5х+1=0 7) 2х2+5х+2=0 8) 3х2+5х+2=0

1) 1/6;1/2 2) 1; 3/2 3) 1; 2/3 4) -2; -3 5) -1/3 ; 1/2 6) -1; -3/2 7) -1; -2/3 8) -2; 3

Разработаны критерии оценки практикума:

За каждое верно выполненное задание ставится 1 балл; Наиболее возможное количество набранных баллов-17 Если ученик набирает:
Менее 7 баллов, то выставляется оценка «2» от 7 до 11 баллов «3» от 12 до 15 баллов «4» от 16-17 баллов «5»

Результаты практикума.

Выполняли работу – 11 человек. Набрали баллов

от 16-17 – 5 человек (45%) от 12-15– 6 человек (55%) Менее 12 – 0 человек

Средний балл – 4,45. Процент качества – 100%

Типичные ошибки, допущенные в работе, связаны с невнимательностью учащихся.

Выводы по результатам проведения практикума

Успешно выполненная работа учащимися 8 класса, позволяет сделать следующие выводы: нестандартные приемы решения квадратных уравнений заслуживают внимания; позволяют экономить время решения, что обусловлено применением тестовой системы экзаменов.

Перейти к содержанию
проекта "Различные способы решения квадратных уравнений"