Индивидуальный проект "Координаты в нашей жизни"
В процессе работы над индивидуальным проектом по математике "Координаты в нашей жизни" учеником 6 класса школы была поставлена и реализована цель, выяснить, где еще кроме математики применяется система координат. Для этого автор дает определение понятиям "координаты" и "система "координат", кратко излагает историю возникновения системы координат.
Подробнее о проекте:
В ученической исследовательской работе по математике "Координаты в нашей жизни" автор рассматривает, в чем заключается основной принцип системы координат и выясняет, в каких областях и сферах нашей жизни не обойтись без системы координат. Также в работе изучено использование координатной плоскости в математике, и проанализирована роль географических координат.
В готовом творческом и исследовательском проекте по математике "Координаты в нашей жизни" автор выполняет практические задания, рассчитанные на построение изображений на координатной плоскости, а также изучает технологию расчета координатных данных для выполнения "рисунка" в прямоугольной системе координат. Предложенный детский проект позволяет научиться свободно ориентироваться на координатной плоскости и на географической карте.
Оглавление
Введение
1. Координаты. Системы координат.
1.1. История возникновения системы координат.
1.2. Координатная плоскость в математике.
1.3. Координаты вокруг нас.
1.4. Географические координаты.
2. Изображения на координатной плоскости.
2.1. Построение изображений на координатной плоскости.
2.2. Создание «рисунков» в прямоугольной системе координат.
Заключение
Приложение
Введение
С координатами в жизни мы сталкиваемся постоянно, можно сказать «на каждом шагу». Идея задавать положение точки на плоскости с помощью чисел зародилась в древности — прежде всего у астрономов и географов при составлении звездных и географических карт, календаря.
Подробное изучение координатной плоскости необходимо. Ведь координаты- это тот же адрес. В повседневной жизни в речи взрослых мы иногда слышим такую фразу: “Оставьте мне свои координаты”. Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, что и считается в этом случае координатами человека. Главное здесь в том, что по этим данным можно найти человека.
Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта. Метод координат позволяет применять средства алгебры и математического анализа при решении геометрических задач. При работе с координатной плоскостью мы неоднократно можем менять расположение точек, размеры единичных отрезков, что требует высокого развития и логического мышления, и, следовательно, способствует его развитию.
В окружающем нас мире существует много явлений и объектов-прообразов, которые можно использовать для составления заданий на метод координат. Если на уроках математики, каждой точке на числовой прямой ставилась в соответствии единственная координата (единственный адрес), то на уроках географии каждой точке на карте соответствуют уже два адреса, две координаты – долгота и широта.
Например, координаты Кемерово: 37,60 восточной долготы и 55,80 северной широты. В математике встречается следующую запись: А (3; 5) – точке А сопоставлены в соответствие два числа, два адреса, две координаты. Так, значит, существует взаимосвязь между математическими координатами и географическими координатами. Весьма интересный материал предоставляет нам астрономия, где каждое созвездие тесно связанно с координатами.
Проблема: С координатами в геометрии мы сталкиваемся постоянно, а где еще применяется метод координат?
Цель: выяснить, где еще кроме математики применяется система координат.
Задачи:
- Познакомиться с историей возникновения системы координат.
- Научиться свободно ориентироваться на координатной плоскости и на географической карте.
- Научиться «рисовать» в прямоугольной системе координат.
История возникновения системы координат
История возникновения координат и системы координат начинается очень давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ученого Анаксимандра Милетского(610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции. Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
Первоначальное применение координат конечно связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта. Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту (см.приложение 1,рис.1).
До наших времён дошла такая история, которая подтолкнула его к открытию. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты.
Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Кроме того, в своей работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. «Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа.
Кроме математики интересы Декарта распространялись на физику, где он дал четкую формулировку закона инерции, открыл закон преломления световых лучей на границе двух различных сред («Диоптрика», 1637).
Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
Координатная плоскость в математике
Каждый объект имеет свой упорядоченный адрес (координаты). Таким образом, адрес или координаты – это числовое или буквенное обозначение того места, где находится объект.
Математиками была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале). Такая модель получила название координатная плоскость.
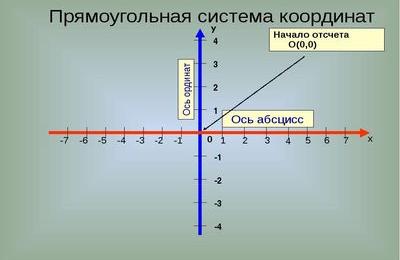
Чтобы из обычной плоскости получить координатную, необходимо начертить две перпендикулярные прямые, отмечая стрелками направления «вправо» и «вверх». На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают Х и называют осью абсцисс, вертикальную прямую обозначают У и называют осью ординат.
Две перпендикулярные оси Х и У с разметкой называют прямоугольной, или декартовой, системой координат. Название «декартова» происходит от фамилии французского философа и математика Рене Декарта, который ее придумал (см.приложение 1,рис. 2).
Для любой точки на координатной плоскости можно указать два числа (координаты). На рисунке показана точка на координатной плоскости. Для получения координат этой точки необходимо через точку провести две прямые, параллельные координатным осям (обозначены пунктирной линией). Пересечение одной из прямых с осью абсцисс – это координата точки, пересечение другой прямой с осью ординат – это координата точки. Сначала указывают координату, потом. Точка имеет координаты. Аналогично находим координаты точки, она имеет координаты.
Координаты вокруг нас
Системы координат пронизывают всю практическую жизнь человека. В нашей речи вы не раз могли слышать такую фразу: «Оставьте мне ваши координаты». Что означает это выражение? Догадались?! Собеседник просит записать свой адрес или номер телефона. У каждого человека бывают ситуации, когда необходимо определить местонахождение: по билету найдите место в зрительном зале или в вагоне поезда.
Координаты окружают нас повсюду:
- чтобы правильно занять свое место в кинотеатре нужно знать две координаты - ряд и место
- система географических координат (широта - параллели и долгота -меридианы)
- те, кто в детстве играл в морской бой, тоже помнят, что каждая клетка на игровом поле определялась двумя координатами - буквой и цифрой
- с помощью координатной сетки летчики, моряки определяют местоположение объектов;
- в биологии - построение схем молекул ДНК, построение диаграмм и графиков, прослеживающих эволюцию развития
- в экономике - разнообразные системы координат применяются для построение графика спроса и предложения, при графическом изображении разных зависимых величин.
- в химии – построение таблицы Менделеева (изменение показателей происходит в горизонтальной и вертикальной плоскости)- взаимное расположение молекул.
- при астрономических наблюдениях координатная сетка накладывается на небесный свод с Землей в центре.
Географические координаты
Так же, как и каждый дом имеет свой адрес (с названием улицы, города), также и каждое место на поверхности Земли можно записать в виде адреса, используя линию широты (параллель) и линию долготы (меридиан), проходящие через это место. Чтобы найти некоторый объект в городе, в большинстве случаев достаточно знать его адрес. Трудности возникают, если нужно объяснить, где находится, например, дачный участок, место в лесу. Универсальным средством указания местоположения служат географические координаты.
При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей.
В современной навигации стандартно используется всемирная система координат WGS-84. В этой системе координат работают все GPS навигаторы и основные картографические проекты в Интернете. Координаты в системе WGS-84 столь же общеупотребимы и понятны всем, как всемирное время.
Местоположение любого объекта на поверхности Земли, его «адрес», определяется географической широтой («адрес» по горизонтали) и географической долготой («адрес» по вертикали). Широта и долгота — это географические координаты точки земной поверхности
Географическая широта. Параллели — это линии широты. Для всех точек одной и той же параллели широта одинакова. Начало отсчета широт — экватор, все точки которого имеют нулевую широту. От экватора широта отсчитывается в градусах вдоль меридиана до заданной точки. Все точки земной поверхности, находящиеся к северу от экватора, имеют северную широту (с. ш.); широта точек к югу от экватора — южная (ю. ш.). Следовательно, широта показывает, насколько далеко к северу или к югу от экватора расположен заданный пункт. Как северная, так и южная широта отсчитываются от 0 до 90° .
Географическая широта заданной точки определяется величиной в градусах дуги меридиана от экватора до параллели, проходящей у точку.
Географическая долгота. Долгота отсчитывается в градусах вдоль параллели. Началом отсчета долгот условно выбран Гринвичский (нулевой, начальный) меридиан, который проходит через старую Гринвичскую обсерваторию в Лондоне. Начальный меридиан и меридиан 180° разделяют Землю на Восточное и Западное полушария.
Все точки Восточного полушария имеют восточную долготу (в. д.), а Западного — западную долготу (з. д.). Как восточная, так и западная долгота отсчитываются от 0 до 180°. Цифры, обозначающие градусы долготы, написаны на глобусе и на карте полушарий у точек пересечения меридианов с экватором. Географическая долгота заданной точки определяется величиной в градусах дуги параллели от начального меридиана до меридиана, проходящего через эту точку.
Построение изображений на координатной плоскости
У древних греков существовала легенда о созвездиях Большой Медведицы и Малой Медведицы:«Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу Калисто, одну из служанок богини Афродиты, вопреки желанию последней. Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в Большую Медведицу, а ее любимую собаку – в Малую Медведицу и взял их на небо».
Существует множество легенд и мифов о созвездиях. Фантазия древних греков поместила их на небо. Так появились созвездия Цефея, Андромеды, Персея и т.д. Знакомство с координатной плоскостью и вид звездного неба натолкнули на мысль, о переносе некоторых созвездий на координатную плоскость.
Созвездие Лев. В этом созвездии запечатлен Немейский Лев, над которым одержал победу Геракл.
Созвездие Близнецы. Созвездие названо в честь двух неразлучных братьев, сыновей Елены Прекрасной – Кастора и Полидевка..
Большая Медведица. Согласно греческому мифу это созвездие олицетворяет прекрасную нимфу Каллисто, превращенную Зевсом в Медведицу, чтобы спасти её от мести Геры.
Малая Медведица. Созвездие известно как Малый Ковш, последняя звезда в "ручке" которого – Полярная.
Орион. В греческой мифологии Орион – сын Посейдона и Эвриалы, великий охотник.
Телец. Созвездие названо в честь быка, на котором Европа переплыла море и попала к Зевсу на Крит.
Создание «рисунков» в прямоугольной системе координат
На координатной плоскости интересно строить рисунки, используя построение графов по координатам. Нужно сначала нарисовать рисунок, а затем его перенести на координатную плоскость, но при этом плавные соединения должны быть в виде отрезков.
Заключение
Таким образом, в результате проведения исследования, мной были решены поставленные задачи. А именно, я изучил координатную плоскость и связанные с ней понятия. Кроме того, мне удалось определить возможность создания графического изображения на координатной плоскости, то есть создать рисунок по известным координатам, а также перенести изображения созвездий с астрономической карты на координатную плоскость.
В результате проведения исследования я доказал, что координатная плоскость используется не только в математике, а пронизывает всю практическую жизнь человека.
В настоящее время координатный метод широко применяется в повседневной жизни. Современные системы спутниковой навигации позволяют определять координаты объекта, а также следить и управлять объектами, в том числе и движущимися. Эта тема также представляет сегодня большой интерес и может стать темой новой исследовательской разработки в будущем.
Приложение
Карточка № 1. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(3;3); (0;3); (-3;2); (-5;2); (-7;4); (-8;3); (-7;1); (-8;-1);
(-7;-2); (-5;0); (-1;-2); (0;-4); (2;-4); (3;-2); (5;-2); (7;0); (5;2);
(3;3); (2;4); (-3;4); (-4;2); глаз (5;0).
Карточка № 2. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(3;0); (1;2); (-1;2); (3;5); (1;7); (-3;6); (-5;7); (-3;4);
(-6;3); (-3;3); (-5;2); (-5;-2); (-2;-3); (-4;-4); (1;-4); (3;-3);
(6;1); (3;0); глаз (-1;5).
Карточка № 3. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(1;7); (0;10); (-1;11); (-2;10); (0;7); (-2;5); (-7;3); (-8;0);
(-9;1); (-9;0); (-7;-2); (-2;-2); (-3;-1); (-4;-1); (-1;3); (0;-2);
(1;-2); (0;0); (0;3); (1;4); (2;4); (3;5); (2;6); (1;9); (0;10); глаз (1;6).
Карточка № 4. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(1;-4); (1;-6); (-4;-6); (-3;-5); (-1;-5); (-3;-4); (-3;-3);
(-1;-1); (-1;0); (-3;0); (-3;-1); (-4;-1); (-4;0); (-3;1); (-1;1);
(-1;2); (-3;3); (-1;4); (0;6); (1;4); (1;2); (3;4); (6;5); (9;2); (9;0);
(9;-4); (6;-4); (5;-1); (4;-1); (1;-4); глаз (-1;3).
Ответы: 1 – утенок; 2 – заяц; 3 – белка; 4 – кошка.
