Индивидуальный проект "Виды и свойства магических квадратов"
В процессе работы над индивидуальным проектом по математике "Виды и свойства магических квадратов" учеником 11 класса школы была поставлена и реализована цель, выяснить различные виды магических квадратов и рассмотреть способы их решения. Автор кратко пересказывает историю возникновения магических квадратов.
Подробнее о проекте:
В ученической исследовательской работе по математике "Виды и свойства магических квадратов" автор рассматривает историю головоломок с магическими квадратами, дает определение и разъясняет способы решения магических квадратов 3х3, магического квадрата Пифагора, магического квадрата Альбрехта Дюрера и латинских квадратов.
В готовом творческом и исследовательском проекте по математике "Виды и свойства магических квадратов" автор демонстрирует решение головоломок с магическими квадратами, выявляет области применения магических квадратов, учится составлять магические квадраты, изучает свойства магических квадратов, которые позволяют определить общие способы их построения.
Оглавление
Введение
1. Магические квадраты.
1.1. История возникновения магических квадратов.
1.2. Магические квадраты 3х3.
1.3. Магический квадрат Пифагора.
1.4. Магический квадрат Альбрехта Дюрера.
1.5. Латинские квадраты.
2. Применение магических квадратов.
Заключение
Список используемых источников
Приложение
Введение
Актуальность проекта: Проблема данного исследования заключается в привлечении обучающихся к решению нестандартных задач и формировании логического мышления, навыков научно-исследовательской работы. Я считаю, что магический квадрат является одной из наиболее интересных головоломок, позволяющей развить логическое мышление.
Великие ученые древности считали количественные отношения основой сущности мира. Они увидели, что числа имеют какую-то самостоятельную жизнь, свои тайны. Поэтому числа и их соотношения занимали величайшие умы человечества. Многие выдающиеся математики посвятили свои работы исследованиям свойств магических квадратов.
Проблема: В чём особенность магических квадратов? Как их заполнять?
Цель работы:
- Выяснить различные виды магических квадратов;
- Рассмотреть способы их решения.
Задачи исследования:
- познакомиться с историей возникновения магических квадратов;
- выявить области применения магических квадратов;
- научиться составлять магические квадраты.
Гипотеза: изучение свойств магических квадратов позволит определить общие способы их построения.
Объект исследования: магические квадраты.
История возникновения магических квадратов
Магический, или волшебный квадрат — это квадратная таблица, заполненная числами так, что сумма чисел в каждой строке, каждом столбике и на обеих диагоналях одинакова. Придуманы магические квадраты впервые, по-видимому, китайцами, так как самое ранее упоминание о них встречается в китайской книге, написанной за 4000-5000 лет до нашей эры. Согласно китайскому преданию, самый простой и древнейший известный человечеству магический квадрат был начертан на панцире священной черепахи.
Если посчитать количество кружочков в каждой фигуре, и поместить полученные числа в клетки квадрата, получится магический квадрат.
Более поздние сведения о магических квадратах относящиеся уже к 1 веку, получены из Индии. Вот один из таких древнеиндийских памятников почти 2000-летней давности.
В таблице 1 16 порядковых чисел размещены в шестнадцати клетках квадрата так, что выполняется основное свойство магического квадрата.
| 1 | 14 | 15 | 4 |
| 12 | 7 | 6 | 9 |
| 8 | 11 | 10 | 5 |
| 13 | 2 | 3 | 16 |
Недаром в ту далёкую эпоху суеверий индийцы, а следом за ними и арабы приписывали этим числовым сочетаниям таинственные и магические свойства. Вся эта своеобразная мозаика чисел с её постоянством сумм действительно придаёт квадрату «волшебную» силу произведения искусства.
Магический квадрат 3х3
В магическом квадрате 3х3 магической постоянной 15 должны быть равны сумме трех чисел по 8 направлениям: по 3 строкам, 3 столбцам и 2 диагоналям. Так как число, стоящее в центре, принадлежит 1 строке, 1 столбцу и 2 диагоналям, оно входит в 4 из 8 троек, дающих в сумме магическую постоянную. Такое число только одно: это 5. Следовательно, число, стоящее в центре магического квадрата 3х3, уже известно: оно равно 5.
Рассмотрим число 9. Оно входит только в 2 тройки чисел. Мы не можем поместить его в угол, так как каждая угловая клетка принадлежит 3 тройкам: строке, столбцу и диагонали. Следовательно, число 9 должно стоять в какой–то клетке, примыкающей к стороне квадрата в ее середине. Из-за симметрии квадрата безразлично, какую из сторон мы выберем, поэтому пишем 9 над числом 5, стоящим в центральной клетке.
По обе стороны от девятки в верхней строке мы можем вписать только числа 2 и 4. Какое из этих двух чисел окажется в правом верхнем углу и какое в левом, опять – таки не имеет значения, так как одно расположение чисел переходит в другое при зеркальном отражении. Остальные клетки заполняются автоматически. Проведенное нами простое построение магического квадрата 3х3 доказывает его единственность.
Такой магический квадрат был у древних китайцев символом огромного значения. Цифра 5 в середине означала землю, а вокруг нее в строгом равновесии располагались огонь (2 и 7), вода (1 и 6), дерево (3 и 8), металл (4 и 9)
Таблица 2
| 6 | 1 | 8 |
| 7 | 5 | 3 |
| 2 | 9 | 4 |
Магический квадрат Пифагора
Великий ученый Пифагор, основавший религиозно – философское учение, провозгласившее количественные отношения основой сущности вещей, считал, что сущность человека заключается тоже в числе – дате рождения. Поэтому с помощью магического квадрата Пифагора можно познать характер человека, степень отпущенного здоровья и его потенциальные возможности, раскрыть достоинства и недостатки и тем самым выявить, что следует предпринять для его совершенствования.
Для того чтобы понять, что такое магический квадрат Пифагора и как подсчитываются его показатели, сделаю его расчет на своем примере. А чтобы убедиться, что результаты подсчета действительно соответствуют реальному характеру той или иной личности, вначале я проверю его на себе.
Для выполнения расчета необходимо рассматривать каждую дату рождения как набор цифр, а не чисел. Запись даты рождения производится в строгой последовательности, однозначные числа записываются без нулей перед ними.
Я родился 2 декабря 2001 года. Запись: число, месяц, год (порядок не нарушать): 2122001.
1. Вычислим первое число: для расчета первого числа необходимо сложить все цифры числового ряда даты рождения 2+1+2+2+0=0+1=8, первое число – 8.
2. Вычислим второе число: для расчета второго числа необходимо сложить цифры, из которых состоит первое число, но у меня получилось однозначное число, значит оставляем просто 8, второе число – 8.
3. Вычислим третье число: для расчета третьего числа необходимо вычесть из первого числа первую цифру всего ряда (в моем примере цифра 2), умноженную на постоянный множитель – 2.
8 – 2 ∙ 2 = 4, третье число – 4.
Вычислим четвертое число. Для вычисления четвертого числа необходимо сложить цифры, из которых состоит третье число, но у меня опять получилось однозначное число, поэтому пишем 4, четвертое число – 4. Запишем полученные числа под датой рождения
| 02122001 |
| 8844 |
Выпишем одинаковые цифры в математический квадрат Пифагора (кроме цифры 0). Для моей даты рождения.
Ячейки квадрата означают следующее:
Ячейка 1 – целеустремленность, воля, упорство, эгоизм.
| 11 | 44 | нет |
| 222 | нет | 88 |
| нет | нет | нет |
1 – законченные эгоисты, стремятся из любого положения извлечь максимальную выгоду.
11 – характер, близкий к эгоистическому.
111 – «золотая середина». Характер спокойный, покладистый, коммуникабельный.
1111 – люди сильного характера, волевые. Мужчины с таким характером подходят на роль военных – профессионалов, а женщины держат свою семью в кулаке.
11111 – диктатор, самодур.
111111 – человек жестокий, способный совершить невозможное; нередко попадает под влияние какой – то идеи.
Ячейка 2 – биоэнергетика, эмоциональность, душевность, чувственность. Количество двоек определяет уровень биоэнергетики.
Двоек нет – открыт канал для интенсивного набора биоэнергетики. Эти люди воспитаны и благородны от природы.
2 – обычные в биоэнергетическом отношении люди. Такие люди очень чувствительны к изменениям в атмосфере.
22 – относительно большой запас биоэнергетики. Из таких людей получаются хорошие врачи, медсестры, санитары. В семье таких людей редко у кого бывают нервные стрессы.
222 – знак экстрасенса.
Ячейка 3 – точность, конкретность, организованность, аккуратность, пунктуальность, чистоплотность, скупость, наклонность к постоянному «восстановлению справедливости».
Нарастание троек усиливает все эти качества. С ними человеку есть смысл искать себя в науках, особенно точных. Перевес троек порождает педантов, людей в футляре.
Ячейка 4 – здоровье. Это связано с экгрегором, то есть энергетическим пространством, наработанным предками и защищающим человека. Отсутствие четверок свидетельствует о болезненности человека.
4 – здоровье среднее, необходимо закалять организм. Из видов спорта рекомендуются плавание и бег.
44 – здоровье крепкое.
444 и более – люди с очень крепким здоровьем.
Ячейка 5 – интуиция, ясновидение, начинающееся проявляться у таких людей уже на уровне трех пятерок.
Пятерок нет – канал связи с космосом закрыт. Эти люди часто ошибаются.
5 – канал связи открыт. Эти люди могут правильно рассчитать ситуацию извлечь из нее максимальную пользу.
55 – сильно развита интуиция. Когда видят «вещие сны», могут предугадывать ход событий. Подходящие для них профессии – юрист, следователь.
555 – почти ясновидящие.
5555 – ясновидящие.
Ячейка 6 – заземлённость, материальность, расчет, склонность к количественному освоению мира и недоверие к качественным скачкам и тем более к чудесам духовного порядка.
Шестерок нет – этим людям необходим физический труд, хотя они его, как правило, не любят. Они наделены неординарным воображением, фантазией, художественным вкусом. Тонкие натуры, они тем не менее способны на поступок.
6 – могут заниматься творчеством или точными науками, но физический труд является обязательным условием существования.
66 – люди очень заземлены, тянутся к физическому труду, хотя как раз для них он не обязателен; желательна умственная деятельность либо занятия искусством.
666 – знак Сатаны, особый и зловещий знак. Эти люди обладают повышенным темпераментом, обаятельны, неизменно становятся в обществе центром внимания.
6666 – эти люди в своих предыдущих воплощениях набрали слишком много заземлённости, они очень много трудились и не представляют свою жизнь без труда. Если в их квадрате естьдевятки, им обязательно нужно заниматься умственной деятельностью, развивать интеллект, хотя бы получить высшее образование.
Ячейка 7 – количество семерок определяет меру таланта.
7 – чем больше они работают, тем больше получают впоследствии.
77 – очень одаренные, музыкальные люди, обладают тонким художественным вкусом, могут иметь склонность к изобразительному искусству.
777 – эти люди, как правило, приходят на Землю ненадолго. Они добры, безмятежны, болезненно воспринимают любую несправедливость. Они чувствительны, любят мечтать, не всегда чувствуют реальность.
7777 – знак Ангела. Люди с таким знаком умирают в младенчестве, а если и живут, то их жизни постоянно угрожает опасность.
Ячейка 8 – карма, долг, обязанность, ответственность. Количество восьмерок определяет степень чувства долга.
Восьмерок нет – у этих людей почти полностью отсутствует чувство долга.
8 – натуры ответственные, добросовестные, точные.
88 – у этих людей развитое чувство долга, их всегда отличает желание помочь другим, особенно слабым, больным, одиноким.
888 – знак великого долга, знак служения народу. Правитель с тремя восьмерками добивается выдающихся результатов.
8888 – эти люди обладают парапсихологическими способностями и исключительной восприимчивостью к точным наукам. Им открыты сверхъестественные пути.
Ячейка 9 – ум, мудрость. Отсутствие девяток - свидетельство того, что умственные способности крайне ограничены.
9 – эти люди должны всю жизнь упорно трудиться, чтобы восполнить недостаток ума.
99 – эти люди умны от рождения. Учатся всегда неохотно, потому что знания даются им легко. Они наделены чувством юмора с ироничным оттенком, независимые.
999 – очень умны. К учению вообще не прикладывают никаких усилий. Прекрасные собеседники.
9999 – этим людям открывается истина. Если у них к тому же развита интуиция, то они гарантированы от провала в любом из своих начинаний. При всем этом они, как правило, довольно приятны, так как острый ум делает их грубыми, немилосердными и жестокими.
Магический квадрат Альбрехта Дюрера
Получение магических квадратов было популярным развлечением среди математиков, создавались огромные квадраты. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Таковым является квадрат из произведения Гете.
А еще существуют квадраты, в которых два числа, расположенных симметрично относительно центра квадрата, дают одинаковую сумму.
Например, квадрат, составленный китайским математиком в XIII в. Он сумел построить магический квадрат из 36 клеток, в котором только две пары таких чисел не дают сумму 37.
| 27 | 29 | 2 | 4 | 13 | 36 |
| 9 | 11 | 20 | 22 | 31 | 18 |
| 32 | 25 | 7 | 3 | 21 | 23 |
| 14 | 16 | 34 | 30 | 12 | 5 |
| 28 | 6 | 15 | 17 | 26 | 19 |
| 1 | 24 | 33 | 35 | 8 | 10 |
В Европу магические квадраты проникли лишь в начале XV века. A в начале XVI века один из них был увековечен выдающимся немецким художником, гравером и немного математиком А. Дюрером в его лучшей гравюре «Меланхолия» (1514 г.). Дюрер воспроизвел на гравюре магический квадрат, составленный из 16 чисел.
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Интересно, что два средних числа в последней строке квадрата (они выделены) составляют год создания гравюры – 1514.
Рассмотрим теперь все свойства этого удивительного квадрата. Но делать это мы будем на другом квадрате, в группу которого входит квадрат Дюрера. Это означает, что квадрат Дюрера получается из того квадрата, который мы будем сейчас рассматривать, одним из семи основных преобразований магических квадратов, а именно поворотом на 180 градусов. Основной квадрат данной группы вы видите в таблице.
| 1 | 14 | 15 | 4 |
| 12 | 7 | 6 | 9 |
| 8 | 11 | 10 | 5 |
| 13 | 2 | 3 | 16 |
Латинские квадраты
Несмотря на то, что математиков интересовали в основном магические квадраты наибольшее применение в науке и технике нашли латинские квадраты.
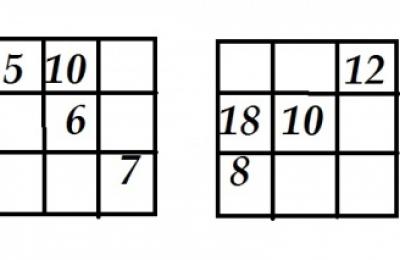
Латинским квадратом называется квадрат n х n клеток, в которых написаны числа 1, 2,…, n, притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу. На рисунке изображены два таких квадрата 4 х 4. Они обладают интересной особенностью: если один квадрат наложить на другой, то все парыполучившихся чисел оказываются различными. Такие пары латинских квадратов называются ортогональными.
| 1 | 2 | 3 | 4 |
| 3 | 4 | 1 | 2 |
| 4 | 3 | 2 | 1 |
| 2 | 1 | 4 | 3 |
| 1 | 2 | 3 | 4 |
| 2 | 1 | 4 | 3 |
| 3 | 4 | 1 | 2 |
| 4 | 3 | 2 | 1 |
Задачу отыскания ортогональных латинских квадратов впервые поставил Л. Эйлер, причём в такой занимательной формулировке: “ Среди 36 офицеров поровну уланов, драгунов, гусаров, кирасиров, кавалергардов и гренадеров и кроме того поровну генералов, полковников, майоров, капитанов, поручиков и подпоручиков, причем каждый род войск представлен офицерами всех шести рангов. Можно ли выстроить всех офицеров в каре 6 х 6 так, чтобы в любой колонне и любой шеренге встречались офицеры всех рангов?”.
Эйлер не смог найти решения этой задачи. В 1901 г. было доказано, что такого решения не существует. В то же время Эйлер доказал, что ортогональные пары латинских квадратов существуют для всех нечетных значений n и для таких четных значений n, которые делятся на 4. Эйлер выдвинул гипотезу, что для остальных значений n, то
В 1901 г. было доказано, что ортогональных квадратов 6 х 6 не существует, и это усиливало уверенность в справедливости гипотезы Эйлера. Однако в 1959 г. помощью ЭВМ были найдены сначала ортогональные квадраты 10 х 10, потом 14 х 14, 18 х 18, 22 х 22. А затем было показано, что для любого n, кроме 6, существуют ортогональные квадраты n х n.
Магические и латинские квадраты – близкие родственники. Пусть мы имеем два ортогональных квадрата. Заполним клетки нового квадрата тех же размеров следующим образом. Поставим туда число n(a – 1)+b, где а - число в такой клетке первого квадрата, а b - число в такой же клетке второго квадрата. Нетрудно понять, что в полученном квадрате суммы чисел в строках и столбцах (но не обязательно на диагоналях) будут одинаковы.
Теория латинских квадратов нашла многочисленные применения как в самой математике, так и в ее приложениях. Использование ортогональных латинских квадратов помогает учесть все возможные варианты в экспериментах в сельском хозяйстве, физике, химии, технике.
Применение магических квадратов
В моей будущей профессиональной деятельности знания о магическом квадрате пригодятся для развития логического мышления, памяти и улучшения концентрации внимания.
Магические квадраты нашли широкое применение в нашей жизни одно из них судоку.
Судоку: японские головоломки. Эту игру, также известную как магический квадрат придумал в 1783году швейцарский математик Леонард Эйлер. Судоку (яп. «су» - число, «доку» - рядом, стоящее отдельно) - японские числовые головоломки, где в квадрате 9х9 клеток нужно расставить числа от 1 до 9 особым образом. В настоящее время судоку широко распространены за пределами Японии: их любят разгадывать как взрослые, так и дети по всему миру.
Важным в процессе обучения математике и информатике студентов технических специальностей является установка связи между теоретическими аспектами математики и возможностями их применения на практике. Для изучения основ программирования удачным является иллюстрация связей между конкретной областью и приложениями математики.
В этом случае перед учащимися стоит определенная целостная задача, цель и актуальность которой им ясна, а не ситуация, когда им предлагается разрозненный набор операций и команд. Грамотно поставленная задача повышает мотивацию учащегося и стимулирует его на быстрейшее ее разрешение. Изучение и использование в обучении информатики магических квадратов открывает определенные перспективы.
Одним из перспективных направлений изучения применения магических квадратов является создание телевизоров, изображение для которых формируется по принципу магического квадрата.
Магические квадраты могут быть применимы в криптографии. Они позволяют создать алгоритм перевода зашифрованного текста в изображение и наоборот. Буквы сообщения расставляются в порядке, заданном магическим квадратом. Затем каждой букве сообщения ставится в соответствие цвет, тем самым в итоге получается изображение.
Заключение
В проекте рассмотрены задачи, связанные с историей развития одного из вопросов математики, занимавшего умы очень многих великих людей, - магических квадратов. Несмотря на то, что собственно магические квадраты не нашли широкого применения в науке и технике, они подвигли на занятия математикой множество незаурядных людей и способствовали развитию других разделов математики (теории групп, определителей, матриц и т. д.).
В проекте также рассмотрен вопрос о квадрате Пифагора, представляющем исторический интерес и, возможно, полезном для составления психологического портрета личности.
Я считаю, что задачи данного исследования решены, я узнал историю возникновения магических квадратов, выявил области их применения и научился составлять их.
Список информационных источников
- М. М. Постников «Магические квадраты. Выпуск 131» Издательство: «URSS» (2017).
- Т. Ушакова «Тренировочные упражнения. Математика. Магические квадраты». Издательство: «Литера ИД» (2017).
- Ю. В. Чебраков «Магические квадраты» С Петербург (1995).
