Индивидуальный проект "Дифференциал и его применение"

В процессе работы над индивидуальным проектом по математике "Дифференциал и его применение" обучающимся техникума была поставлена цель изучить дифференциалы и его приложения. Автор дает определение дифференциалу, описывает свойства дифференциала и области его использования, объясняет, как решать задачи с дифференциалами.
Подробнее о проекте:
В ученической исследовательской работе по математике "Дифференциал и его применение" автор рассматривает математические правила использования дифференциалов в решении задач, узнает о приложениях дифференциалов и выясняет область их применения. В практической части проекта представлены задачи различного содержания (экономического, химического и т.д.).
В готовом исследовательском проекте по математике "Дифференциал и его применение" автор рассматривает одно наиболее фундаментальное и показательное основание – возникновение дифференциального исчисления. В работе изучены: дифференциал функции, приближенные вычисления с применением дифференциала, приближенные вычисления с помощью дифференциала функции одной переменной, абсолютная и относительная погрешность вычислений. Дана оценка погрешности формул при помощи применения дифференциала и рассмотрены разные формы записи дифференциала.
Оглавление
Введение
1. Возникновение понятия дифференциала.
2. Понятие дифференциала функции. Свойства. Применение дифференциала в приближенных вычислениях.
3. Современное определение.
4. Механическое истолкование.
5. Производная и дифференциал.
6. Геометрическая интерпретация.
7. Что более универсально: приращение аргумента или его дифференциал?
8. Замена приращений дифференциалами.
9. Дифференциал функции. Примеры.
10. Приближенные вычисления с применением дифференциала.
11. Приближенные вычисления с помощью дифференциала функции одной переменной.
12. Абсолютная и относительная погрешность вычислений.
13. Оценка погрешности формул при помощи применения дифференциала.
14. Почему дифференциал можно использовать в приближенных вычислениях?
15. О разных формах записи дифференциала.
Заключение
Литература
Введение
В проекте рассматриваются понятия дифференциалов и их применение в различных областях науки. В практической части проекта представлены задачи различного содержания (экономического, химического и т.д.).
Наряду с производными функций их дифференциалы – это одни из базовых понятий дифференциального исчисления, основного раздела математического анализа.
Являясь неразрывно связанными между собой, оба они уже несколько столетий активно используются при решении практически всех задач, которые возникали в процессе научно-технической деятельности человека. В современном научном сообществе принято однозначно разделять науку на античный период и период нового времени.
Но в чём же состоит отличие этих периодов? Чем принципиально отличался научный подход Платона, Аристотеля и прочих известных учёных античности от подхода крупных деятелей науки нового времени? В реальности, у разделения на два периода существует множество оснований.
В рамках данного проекта мы рассмотрим одно, наиболее фундаментальное и показательное основание – возникновение дифференциального исчисления. Через предпосылки к появлению этого известнейшего метода в современной науке в трудах философов и математиков мы сможем проследить чёткую границу между античным и современным взглядом на науку, однозначно ответив на поставленные в начале статьи вопросы.
Рубеж XVI-XVII вв. в истории науки действительно был переломным моментом, когда европейская наука совершила качественный скачок. В это время был совершен переход от античной науки к науке нового времени.
Ни для кого не секрет, что «локомотивами» прогресса в рассматриваемый период были такие великие учёные как Рене Декарт, Галилео Галилей, Иоганн Кеплер, Бонавентура Кавальери, Исаак Ньютон. Каждый из них сказал свое новое слово в механике, математике, астрономии и прочих дисциплинах. Но не столько важны их заслуги в отдельных науках, сколько важен вклад в формирование методологии науки нового времени.
Плоды трудов этих известных ученых в области методологии науки имели широкое распространение, и многие из них по сей день остаются основополагающими принципами современной науки. Легче всего связь методологических достижений самых крупных деятелей науки XVI-XVII вв. можно проследить именно через историю возникновения дифференциального исчисления и «принцип непрерывности», так или иначе встречающийся в трудах Кеплера, Кавальери, Декарта, а позднее Ньютона.
Цель проекта: изучить дифференциалы и его приложения.
Задачи проекта:
- Научиться решать задачи с дифференциалами;
- Узнать о приложениях дифференциалов;
- Выяснить область применения дифференциалов
Основополагающий вопрос: Что такое дифференциалы и их приложения?
Проблемные вопросы:
- Что такое дифференциал?
- Какие свойства у дифференциала?
- Как решать задачи с дифференциалами?
- Где используют дифференциалы?
Возникновение понятия дифференциала
Впервые разъяснил, что такое дифференциал, один из создателей (наряду с Исааком Ньютоном) дифференциального исчисления знаменитый немецкий математик Готфрид Вильгельм Лейбниц. До этого математиками 17 ст. использовалось весьма нечеткое и расплывчатое представление о некоторой бесконечно малой «неделимой» части любой известной функции, представлявшей очень малую постоянную величину, но не равную нулю, меньше которой значения функции быть просто не могут.
Отсюда был всего один шаг до введения представления о бесконечно малых приращениях аргументов функций и соответствующих им приращениях самих функций, выражаемых через производные последних. И этот шаг был сделан практически одновременно двумя вышеупомянутыми великими учеными.

Исходя из необходимости решения насущных практических задач механики, которые ставила перед наукой бурно развивающаяся промышленность и техника, Ньютон и Лейбниц создали общие способы нахождения скорости изменения функций (прежде всего применительно к механической скорости движения тела по известной траектории), что привело к введению таких понятий, как производная и дифференциал функции, а также нашли алгоритм решения обратной задачи, как по известной (переменной) скорости найти пройденный путь, что привело к появлению понятия интеграла.
В трудах Лейбница и Ньютона впервые появилось представление о том, что дифференциалы - это пропорциональные приращениям аргументов Δх основные части приращений функций Δу, которые могут быть с успехом применены для вычисления значений последних. Иначе говоря, ими было открыто, что приращение функции может быть в любой точке (внутри области ее определения) выражено через ее производную как Δу = y'(x) Δх + αΔх, где α Δх – остаточный член, стремящийся к нулю при Δх→0, гораздо быстрее, чем само Δх.
Согласно основоположникам матанализа, дифференциалы – это как раз и есть первые члены в выражениях приращений любых функций. Еще не обладая четко сформулированным понятием предела последовательностей, они интуитивно поняли, что величина дифференциала стремится к производной функции при Δх→0 - Δу/Δх→ y'(x).
В отличие от Ньютона, который был прежде всего физиком, и рассматривал математический аппарат как вспомогательный инструмент исследования физических задач, Лейбниц уделял большее внимание самому этому инструментарию, включая и систему наглядных и понятных обозначений математических величин. Именно он предложил общепринятые обозначения дифференциалов функции dy = y'(x)dx, аргумента dx и производной функции в виде их отношения y'(x) = dy/dx.
Понятие дифференциала функции
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать у/ х=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.
Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых ƒ'(х)•∆х и а•∆х, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:
Поэтому первое слагаемое ƒ'(х) ∆х называют главной частью приращения функции ∆у.
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х. (1)
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у'=х'=1, то, согласно формуле (1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (1) можно записать так:
dy=ƒ'(х)dх, (2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (2) следует равенство dy/dx=ƒ'(х). Теперь обозначение
производной dy/dx можно рассматривать как отношение дифференциалов dyиdх.
Дифференциал обладает следующими основными свойствами.
Форма дифференциала инвариантна (неизменна): он всегда равен произведению производной функции на дифференциал аргумента, независимо от того, простым или сложным является аргумент.
Применение дифференциала к приближенным вычислениям
Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство
∆у≈dy, (3)
причем это равенство тем точнее, чем меньше ∆х.
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (3) широко применяется в вычислительной практике.
Современное определение
Что такое дифференциал с точки зрения современной математики? Он тесно связан с понятием приращения переменной величины. Если переменная y принимает сначала значение y = y1, а затем y = y2, то разность y2 ─ y1 называется приращением величины y.
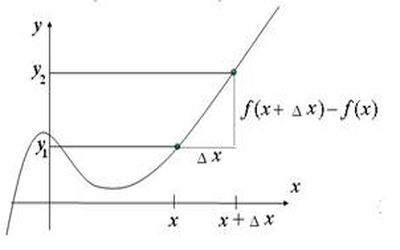
Приращение может быть положительным.отрицательным и равным нулю. Слово «приращение» обозначается Δ, запись Δу (читается «дельта игрек») обозначает приращение величины y. так что Δу = y2 ─ y1.
Если величину Δу произвольной функции y = f (x) возможно представить в виде Δу = A Δх + α, где у A нет зависимости от Δх, т. е. A = const при данном х, а слагаемое α при Δх→0 стремится к нему же еще быстрее, чем само Δх, тогда первый («главный») член, пропорциональный Δх, и является для y = f (x) дифференциалом, обозначаемым dy или df(x) (читается «дэ игрек», «дэ эф от икс»). Поэтому дифференциалы – это «главные» линейные относительно Δх составляющие приращений функций.
Механическое истолкование
Пусть s = f (t) – расстояние прямолинейно движущейся материальной точки от начального положения (t – время пребывания в пути). Приращение Δs – это путь точки за интервал времени Δt, а дифференциал ds = f' (t) Δt – это путь, который точка прошла бы за то же время Δt, если бы она сохранила скорость f'(t), достигнутую к моменту t.
При бесконечно малом Δt воображаемый путь ds отличается от истинногоΔs на бесконечно малую величину, имеющую высший порядок относительно Δt. Если скорость в момент t не равна нулю, то ds дает приближенную величину малого смещения точки.
Производная и дифференциал
Коэффициент A в первом слагаемом выражения приращения функции равен величине ее производной f '(x). Таким образом, имеет место следующее соотношение - dy = f '(x)Δх, или же df (x) = f '(x)Δх. Известно, что приращение независимого аргумента равно его дифференциалу Δх = dx. Соответственно, можно написать: f '(x) dx = dy. Нахождение (иногда говорят, «решение») дифференциалов выполняется по тем же правилам, что и для производных. Перечень их приведен ниже.
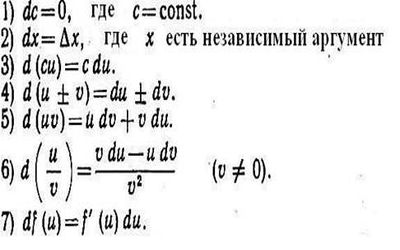
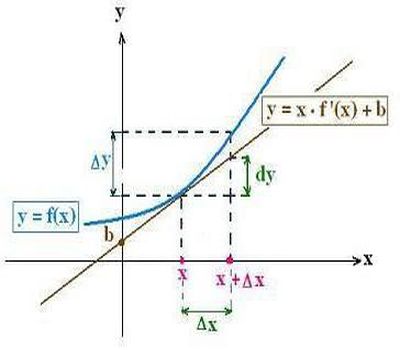
Геометрическая интерпретация
Дифференциал функции y = f (x) равен произведению её производной на приращение независимой переменной x (аргумента).
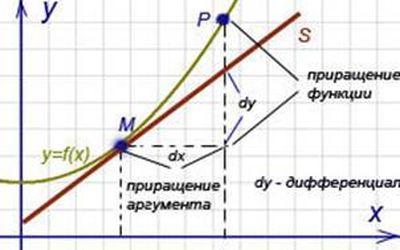
Дифференциал функции y = f (x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину (см. рисунок).
Итак, графически дифференциал произвольной функции равен величине приращения ординаты ее касательной.
Что более универсально: приращение аргумента или его дифференциал?
Здесь необходимо сделать некоторые пояснения. Представление величиной f '(x)Δх дифференциала возможно при рассмотрении х в качестве аргумента. Но функция может быть сложной, в которой х может быть функцией некоторого аргумента t. Тогда представление дифференциала выражением f '(x)Δх, как правило, невозможно; кроме случая линейной зависимости х = at + b.
Что же касается формулы f '(x)dx= dy, то и в случае независимого аргумента х (тогда dx = Δх), и в случае параметрической зависимости х от t, она представляет дифференциал.
Например, выражение 2 x Δх представляет для y = x2 ее дифференциал, когда х есть аргумент. Положим теперь х= t2 и будем считать t аргументом. Тогда y = x2 = t4.
Далее следует (t +Δt)2 = t2 + 2tΔt + Δt2. Отсюда Δх = 2tΔt + Δt2. Значит: 2xΔх = 2t2 (2tΔt + Δt2 ).
Это выражение не пропорционально Δt и потому теперь 2xΔх не является дифференциалом. Его можно найти из уравнения y = x2 = t4. Он оказывается равен dy=4t3Δt.
Если же взять выражение 2xdx, то оно представляет дифференциал y = x2 при любом аргументе t. Действительно, при х= t2 получим dx = 2tΔt.
Значит 2xdx = 2t22tΔt = 4t3Δt, т. е. выражения дифференциалов, записанные через две разные переменные, совпали.
Замена приращений дифференциалами
Если f '(x) ≠ 0, то Δу и dy эквивалентны (при Δх→0); при f '(x) = 0 (что означает и dy = 0), они не эквивалентны.
Например, если y = x2, то Δу = (x + Δх)2 ─ x2= 2xΔх + Δх2, а dy=2xΔх. Если х=3, то имеем Δу = 6Δх + Δх2 и dy = 6Δх, которые эквивалентны вследствие Δх2→0, при х=0 величины Δу = Δх2 и dy=0 не эквивалентны.
Этот факт, вместе с простой структурой дифференциала (т. е. линейности по отношению к Δх), часто используется в приближенных вычислениях, в предположении, что Δу ≈ dy для малых Δх. Найти дифференциал функции, как правило, легче, чем вычислить точное значение приращения.
Например, имеем металлический куб с ребром х=10,00 см. При нагревании ребро удлинилось на Δх = 0,001 см. Насколько увеличился объем V куба? Имеем V = х2, так что dV = 3x2Δх = 3∙102∙0/01 = 3 (см3).
Увеличение объема ΔV эквивалентно дифференциалу dV, так что ΔV = 3 см3. Полное вычисление дало бы ΔV =10,013 ─ 103 = 3,003001. Но в этом результате все цифры, кроме первой ненадежны; значит, все равно, нужно округлить его до 3 см3.
Очевидно, что такой подход является полезным, только если возможно оценить величину привносимой при этом ошибки.
Дифференциал функции
Попробуем найти дифференциал функции y = x3, не находя производной. Дадим аргументу приращение и определим Δу.
Δу = ( Δх + x)3 ─ x3 = 3x2Δх + (3xΔх2 + Δх3).
Здесь коэффициент A= 3x2 не зависит от Δх, так что первый член пропорционален Δх, другой же член 3xΔх2 + Δх3 при Δх→0 уменьшается быстрее, чем приращение аргумента. Стало быть, член 3x2Δх есть дифференциал y = x3:
dy=3x2Δх=3x2dx или же d(x3) = 3x2dx.
При этом d(x3) / dx = 3x2.
Найдем теперь dy функции y = 1/x через ее производную. Тогда d(1/x) / dx = ─1/х2. Поэтому dy = ─ Δх/х2. Дифференциалы основных алгебраических функций приведены ниже.
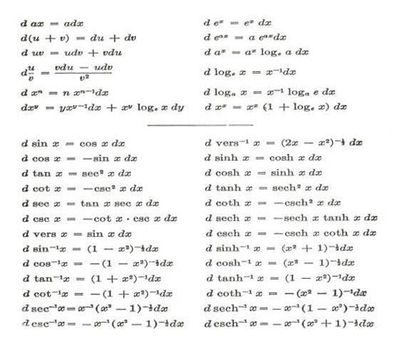
Приближенные вычисления с применением дифференциала
Вычислить функцию f (x), а также ее производную f '(x) при x=a часто нетрудно, а вот сделать то же самое в окрестности точки x=a бывает нелегко. Тогда на помощь приходит приближенное выражение f(a + Δх) ≈ f '(a)Δх + f(a).
Оно дает приближенное значение функции при малых приращениях Δх через ее дифференциал f '(a)Δх.
Следовательно, данная формула дает приближенное выражение для функции в конечной точке некоторого участка длиной Δх в виде суммы ее значения в начальной точке этого участка (x=a) и дифференциала в той же начальной точке. Погрешность такого способа определения значения функции иллюстрирует рисунок ниже.
Однако известно и точное выражение значения функции для x=a+Δх, даваемое формулой конечных приращений (или, иначе, формулой Лагранжа)
f(a+ Δх) ≈ f '(ξ) Δх + f(a), где точка x = a+ ξ находится на отрезке от x = a до x = a + Δх, хотя точное положение ее неизвестно. Точная формула позволяет оценивать погрешность
приближенной формулы. Если же в формуле Лагранжа положить ξ = Δх /2, то хотя она и перестает быть точной, но дает, как правило, гораздо лучшее приближение, чем исходное выражение через дифференциал.
Приближенные вычисления с помощью дифференциала функции одной переменной
Пример 1
Вычислить приближенно, заменяя приращения функции ее дифференциалом.
Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала.
Начинаем разбираться, здесь всё просто!
На первом этапе необходимо составить функцию. По условию предложено вычислить кубический корень из числа, поэтому соответствующая функция имеет вид. Нам нужно с помощью формулы найти приближенное значение.
Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе: получилось 4 с хвостиком, это важный ориентир для решения.
Подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение должно быть как можно ближе к 67. В данном случае.
Примечание: Когда с подбором всё равно возникает затруднение, просто посмотрите на скалькулированное значение, возьмите ближайшую целую часть (в данном случае 4) и возведите её
16 нужную в степень. В результате и будет выполнен нужный подбор.
Если, то приращение аргумента.
Итак, число 67 представлено в виде суммы.
Далее работаем с правой частью формулы.
Сначала вычислим значение функции в точке. Собственно, это уже сделано ранее.
Пример 2.
Вычислить приближенно, заменяя приращения функции ее дифференциалом.
Это пример для самостоятельного решения. Примерный образец чистового оформления и ответ в конце урока. Начинающим сначала рекомендую вычислить точное значение на микрокалькуляторе, чтобы выяснить, какое число принять за, а какое – за.
У некоторых, возможно, возник вопрос, зачем нужна эта задача, если можно всё спокойно и более точно подсчитать на калькуляторе? Согласен, задача глупая и наивная. Но попытаюсь немного её оправдать. Во-первых, задание иллюстрирует смысл дифференциала функции. Во-вторых, в древние времена, калькулятор был чем-то вроде личного вертолета в наше время.
Сам видел, как из местного политехнического института году где-то в 1985-86 выбросили компьютер размером с комнату (со всего города сбежались радиолюбители с отвертками, и через пару часов от агрегата остался только корпус). Антиквариат водился и у нас на физмате, правда, размером поменьше – где-то с парту. Вот так вот и мучились наши предки с методами приближенных вычислений. Конная повозка – тоже транспорт.
Так или иначе, задача осталась в стандартном курсе высшей математики, и решать её придётся. Это основной ответ на ваш вопрос =)
Пример 3.
Вычислить приближенно с помощью дифференциала значение функции в точке. Вычислить более точное значение функции в точке с помощью микрокалькулятора, оценить абсолютную и относительную погрешность вычислений.
Фактически то же самое задание, его запросто можно переформулировать так: «Вычислить приближенное значение с помощью дифференциала»
Решение: Используем знакомую формулу. В данном случае уже дана готовая функция.
Значение необходимо представить в виде. Ну, тут легче, мы видим, что число 1,97 очень близко к «двойке». И, следовательно. Вычислим значение функции в точке.
Используя формулу, вычислим дифференциал в этой же точке.
Находим первую производную. И её значение в точке. Таким образом, дифференциал в точке. В результате, по формуле. Вторая часть задания состоит в том, чтобы найти абсолютную и относительную погрешность вычислений.
Абсолютная и относительная погрешность вычислений. Абсолютная погрешность вычислений находится по формуле.
Знак модуля показывает, что нам без разницы, какое значение больше, а какое меньше. Важно, насколько далеко приближенный результат отклонился от точного значения в ту или иную сторону.
Относительная погрешность вычислений находится по формуле или, то же самое.
Относительная погрешность показывает, на сколько процентов приближенный результат отклонился от точного значения. Существует версия формулы и без домножения на 100%, но на практике я почти всегда вижу вышеприведенный вариант с процентами.
После короткой справки вернемся к нашей задаче, в которой мы вычислили приближенное значение функции с помощью дифференциала.
Вычислим точное значение функции с помощью микрокалькулятора, строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются.
Вычислим абсолютную погрешность. Вычислим относительную погрешность, получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение.
Ответ, абсолютная погрешность вычислений, относительная погрешность вычислений. Оценка погрешности формул при помощи применения дифференциала.
Измерительные инструменты в принципе неточны, и привносят в данные измерений, соответствующие ошибки. Их характеризуют предельной абсолютной погрешностью, или, короче, предельной погрешностью – положительным числом, заведомо превышающим эту ошибку по абсолютной величине (или в крайнем случае равным ей). Предельной относительной погрешностью называют частное от ее деления на абсолютное значение измеренной величины.
Пусть точная формула y= f (x) использована для вычисляения функции y, но значение x есть результат измерения и поэтому привносит в y ошибку. Тогда, чтобы найти предельную абсолютную погрешность
│Δу│функции y, используют формулу
│Δу│≈│dy│=│ f '(x)││Δх│,
где │Δх│является предельной погрешностью аргумента. Величину │Δу│ следует округлить в сторону увеличения, т.к. неточной является сама замена вычисления приращения на вычисление дифференциала.
Почему дифференциал можно использовать в приближенных вычислениях?
Дифференциал является главной, линейной относительно частью приращения функции; чем меньше, тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях приращение функции можно приближенно заменить его главной частью.
Дифференциал функции в точке x.
Замечание. Нужно помнить, что если x – исходное значение аргумента, а - наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
Заключение
Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Здесь, может быть, уместно вспомнить слова А. Пуанкаре: "Математика - это искусство давать разным вещам одно наименование".
Эти слова являются выражением того, что математика изучает одним методом, с помощью математической модели, различные явления действительного мира. Изучая какие-либо физические явления, исследователь, прежде всего, создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Математическая модель дает возможность изучать явление в целом, предсказать его развитие, делать количественные оценки изменений, происходящих в нем с течением времени.
На протяжении всей работы мы, безусловно, ознакомились с теорией о дифференциалах, разъяснили для себя, что это такое дифференциалы, как они решаются и в каких областях науки они применяются. Очень многое показалось нам сложным и не совсем понятным в силу нашего пока еще не очень совершенного математического аппарата, но, надеемся, что в дальнейшем наше первичное знакомство с данной темой явится основой для более серьезных исследований в этой области.
Поставленные в проекте задачи выполнен.
Список использованных источников
- Эрроусмит Д., Плейс К. Качественная теория с приложениями. М., 1986
- Интернет.
